
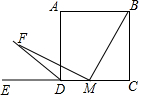
 如图,在正方形ABCD中,AB=2,点M为正方形ABCD的边CD上的动点(与点C,D不重合),连接BM,作MF⊥BM,与正方形ABCD的外角∠ADE的平分线交于点F.设CM=x,△DFM的面积为y,则y与x之间的函数关系式y=-$\frac{1}{2}$x2+x.
如图,在正方形ABCD中,AB=2,点M为正方形ABCD的边CD上的动点(与点C,D不重合),连接BM,作MF⊥BM,与正方形ABCD的外角∠ADE的平分线交于点F.设CM=x,△DFM的面积为y,则y与x之间的函数关系式y=-$\frac{1}{2}$x2+x. 分析 在BC上截取CH=CM,连接MH,则△MCH是等腰直角三角形,BH=MD,证出∠BHM=∠MDF,∠1=∠2,由ASA证明△BHM≌△MDF,再根据三角形面积公式求解即可.
解答 证明:∵四边形ABCD是正方形,
∴CD=BC,∠C=∠CDA=90°=∠ADE,
∵DF平分∠ADE,
∴∠ADF=$\frac{1}{2}$∠ADE=45°,
∴∠MDF=90°+45°=135°.
在BC上截取CH=CM,连接MH,如图,则△MCH是等腰直角三角形,BH=MD,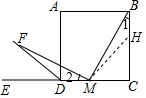 ∴∠CHM=∠CMH=45°,
∴∠CHM=∠CMH=45°,
∴∠BHM=135°,
∴∠1+∠HMB=45°,∠BHM=∠MDF,
∵FM⊥BM,
∴∠FMB=90°,
∴∠2+∠BMH=45°,
∴∠1=∠2.
在△BHM与△MDF中,
$\left\{\begin{array}{l}{∠1=∠2}\\{BH=MD}\\{∠BHM=∠MDF}\end{array}\right.$,
∴△BHM≌△MDF(ASA),
∴BH=MD=2-x,
∴y与x之间的函数关系式为y=$\frac{1}{2}$x(2-x)=-$\frac{1}{2}$x2+x.
故答案为:y=-$\frac{1}{2}$x2+x.
点评 本题考查了根据实际问题列二次函数关系式,正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.


科目:初中数学 来源: 题型:解答题
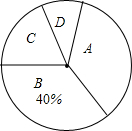 2017年2月8日晚,央视一套播出感动中国2016年度人物颁奖盛典,三入火海救人的南阳人王峰的当选,在中原大地引起强烈反响,社会各界纷纷表达对英雄的敬意,厚重的历史文化,历代先贤的故事,层出不穷的“河南好人”潜移默化地影响着中原儿女,为了弘扬中原优秀传统文化,某中学举办了中原文化知识大赛,并随机抽取了50名学生的成绩(得分为整数),将他们的得分按优秀、良好、及格、不及格(分别用A,B,C,D表示)四个等级进行统计,并绘制成下面的统计表和扇形统计图:
2017年2月8日晚,央视一套播出感动中国2016年度人物颁奖盛典,三入火海救人的南阳人王峰的当选,在中原大地引起强烈反响,社会各界纷纷表达对英雄的敬意,厚重的历史文化,历代先贤的故事,层出不穷的“河南好人”潜移默化地影响着中原儿女,为了弘扬中原优秀传统文化,某中学举办了中原文化知识大赛,并随机抽取了50名学生的成绩(得分为整数),将他们的得分按优秀、良好、及格、不及格(分别用A,B,C,D表示)四个等级进行统计,并绘制成下面的统计表和扇形统计图:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | 0.38 |
| B | 75~89 | m | x |
| C | 60~74 | n | y |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
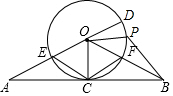 如图,在△OAB中,OA=OB,以点O为圆心的⊙O经过AB的中点C,直线AO与⊙O相交于点E、D,OB交⊙O于点F,P是$\widehat{DF}$的中点,连接CE、CF、BP.
如图,在△OAB中,OA=OB,以点O为圆心的⊙O经过AB的中点C,直线AO与⊙O相交于点E、D,OB交⊙O于点F,P是$\widehat{DF}$的中点,连接CE、CF、BP.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
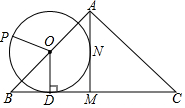 如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N.
如图,在△ABC中,AB=AC,点O为边AB的中点,OD⊥BC于点D,AM⊥BC于点M,以点O为圆心,线段OD为半径的圆与AM相切于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 完成下面推理过程.
完成下面推理过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com