
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,
两点,![]() ,交
,交![]() 轴于点
轴于点![]() ,对称轴是直线
,对称轴是直线![]() .
.
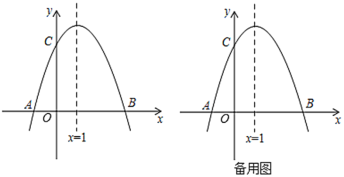
(1)求抛物线的解析式及点![]() 的坐标;
的坐标;
(2)连接![]() ,
,![]() 是线段
是线段![]() 上一点,
上一点,![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 正好落在
正好落在![]() 上,求点
上,求点![]() 的坐标;
的坐标;
(3)动点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向点
出发,以每秒2个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() (
(![]() )秒.若
)秒.若![]() 与
与![]() 相似,请求出
相似,请求出![]() 的值.
的值.
科目:初中数学 来源: 题型:
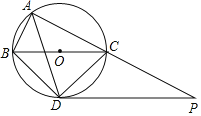
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在 10×6 的正方形网格中,每个小正方形的边长均为 1,线段 AB 的端点 A、B 均在小正方形的顶点上.
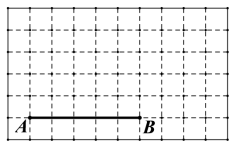
(1)在图中画出以 AB 为一腰的等腰△ABC,点 C 在小正方形顶点上,△ABC 为钝角三角形,且△ABC 的面积为![]() ;
;
(2)在图中画出以 AB 为斜边的直角三角形 ABD, 点 D在小正方形的顶点上,且 AD>BD;
(3)连接 CD,请你直接写出线段 CD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以AB为直径的⊙O交∠BAD的平分线于点C,交AD于点F,过点C作CD⊥AD于D,交AB的延长线于点E.
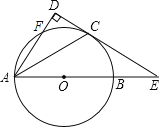
(1)求证:CD为⊙O的切线;
(2)若![]() =
=![]() ,求cos∠DAB的值.
,求cos∠DAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某童装专卖店在销售中发现,一款童装每件进价为40元,若销售价为60元,每天可售出20件,为迎接“双十一”,专卖店决定采取适当的降价措施,以扩大销售量,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件![]() 设每件童装降价x元
设每件童装降价x元![]() 时,平均每天可盈利y元.
时,平均每天可盈利y元.
![]() 写出y与x的函数关系式;
写出y与x的函数关系式;
![]() 当该专卖店每件童装降价多少元时,平均每天盈利400元?
当该专卖店每件童装降价多少元时,平均每天盈利400元?
![]() 该专卖店要想平均每天盈利600元,可能吗?请说明理由.
该专卖店要想平均每天盈利600元,可能吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
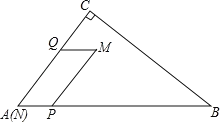
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒1个单位的速度向终点
以每秒1个单位的速度向终点![]() 运动;同时,点
运动;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以每秒2个单位的速度向终点
以每秒2个单位的速度向终点![]() 运动,当
运动,当![]() 、
、![]() 两点其中一点到达点
两点其中一点到达点![]() 时,另一点也随之停止运动,过点
时,另一点也随之停止运动,过点![]() 作
作![]() ,过点
,过点![]() 作
作![]() .当点
.当点![]() 与点
与点![]() 不重合时,以
不重合时,以![]() 、
、![]() 为邻边作
为邻边作![]() .设
.设![]() 、
、![]() 两点的运动时间为
两点的运动时间为![]() 秒.
秒.
(1)求线段![]() 的长.(用含
的长.(用含![]() 的代数式表示)
的代数式表示)
(2)点![]() 在边
在边![]() 上运动,当点
上运动,当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的值.
的值.
(3)设![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,当点
,当点![]() 在
在![]() 内部时,求
内部时,求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当![]() 的一边是它邻边2倍时,直接写出
的一边是它邻边2倍时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
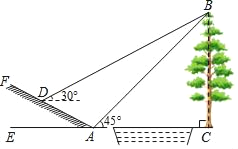
【题目】如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡AF上的D处测得大树顶端B的仰角是30°,在地面上A处测得大树顶端B的仰角是45°.若坡角∠FAE=30°,AD=6m,求大树的高度.(结果保留整数,参考数据:![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三瓶不同浓度的酒精,A瓶内有酒精2kg,浓度x%,B瓶有酒精3kg,浓度y%,C瓶有酒精5kg,浓度z%,从A瓶中倒出10%,B瓶中倒出20%,C瓶中倒出24%,混合后测得浓度33.5%,将混合后的溶液倒回瓶中,使它们恢复原来的质量,再从A瓶倒出30%,B瓶倒出30%,C瓶倒出30%,混合后测得浓度为31.5%,测量发现![]() ,
,![]() ,
,![]() ,且x、y、z均为整数,则把起初A、B两瓶酒精全部混合后的浓度为______.
,且x、y、z均为整数,则把起初A、B两瓶酒精全部混合后的浓度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
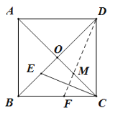
【题目】如图,边长为2的正方形ABCD的对角线AC与BD交于点O,将正方形ABCD沿DF直线折叠,点C落在对角线BD上的点E处,折痕DF交AC于点M,则OM的长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com