
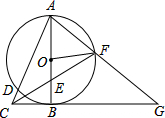
 如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在$\widehat{AB}$的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在$\widehat{AB}$的中点,连接AF并延长与CB的延长线相交于点G,连接OF.分析 (1)直接利用圆周角定理结合平行线的判定方法得出FO是△ABG的中位线,即可得出答案;
(2)首先得出△FOE≌△CBE(ASA),则BC=FO=$\frac{1}{2}$AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
解答 (1)证明:∵以Rt△ABC的直角边AB为直径作⊙O,点F恰好落在$\widehat{AB}$的中点,
∴$\widehat{AF}$=$\widehat{BF}$,
∴∠AOF=∠BOF,
∵∠ABC=∠ABG=90°,
∴∠AOF=∠ABG,
∴FO∥BG,
∵AO=BO,
∴FO是△ABG的中位线,
∴FO=$\frac{1}{2}$BG;
(2)解:在△FOE和△CBE中,
$\left\{\begin{array}{l}{∠FOE=∠CBE}\\{EO=BE}\\{∠OEF=∠CEB}\end{array}\right.$,
∴△FOE≌△CBE(ASA),
∴BC=FO=$\frac{1}{2}$AB=2,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{5}$,
连接DB,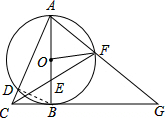 ∵AB为⊙O直径,
∵AB为⊙O直径,
∴∠ADB=90°,
∴∠ADB=∠ABC,
∵∠BCD=∠ACB,
∴△BCD∽△ACB,
∴$\frac{BC}{AC}$=$\frac{CD}{BC}$,
∴$\frac{2}{2\sqrt{5}}$=$\frac{DC}{2}$,
解得:DC=$\frac{2\sqrt{5}}{5}$.
点评 此题主要考查了相似三角形的判定与性质以及全等三角形的判定与性质等知识,正确得出△BCD∽△ACB是解题关键.


科目:初中数学 来源: 题型:解答题
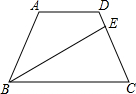 如图,在等腰梯形ABCD中,AD∥BC,AD=1,BC=3,∠ABC的平分线交腰CD于点E(不与点C、D重合).
如图,在等腰梯形ABCD中,AD∥BC,AD=1,BC=3,∠ABC的平分线交腰CD于点E(不与点C、D重合).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 | 甲 | 乙 |
| 原料成本 | 12 | 8 |
| 销售单价 | 18 | 12 |
| 生产提成 | 1 | 0.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为2$\sqrt{3}$.
如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
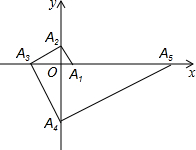 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015.
如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
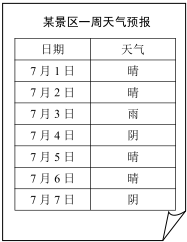 某景区7月1日-7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率:
某景区7月1日-7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com