
 ,两车同时到达抢修点,所用时间相等,利用这个条件建立等量关系,列方程.
,两车同时到达抢修点,所用时间相等,利用这个条件建立等量关系,列方程.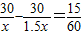


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源:2008年全国中考数学试题汇编《图形的相似》(04)(解析版) 题型:解答题
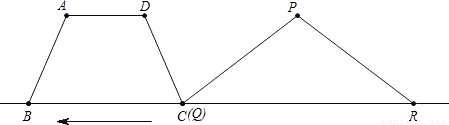
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《二次函数》(09)(解析版) 题型:解答题
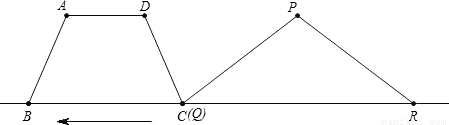
查看答案和解析>>
科目:初中数学 来源:2010年山东省泰安市新泰市第一教研区中考数学预测卷(二)(解析版) 题型:解答题
 (2008•广州)如图,一次函数y=kx+b的图象与反比例函数y=
(2008•广州)如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A、B两点.
的图象相交于A、B两点.查看答案和解析>>
科目:初中数学 来源:2009年广东省中考数学模拟试卷(B卷)(解析版) 题型:解答题
 (2008•广州)如图,一次函数y=kx+b的图象与反比例函数y=
(2008•广州)如图,一次函数y=kx+b的图象与反比例函数y= 的图象相交于A、B两点.
的图象相交于A、B两点.查看答案和解析>>
科目:初中数学 来源:2009年广东省汕头市潮南区中考数学模拟试卷(解析版) 题型:解答题
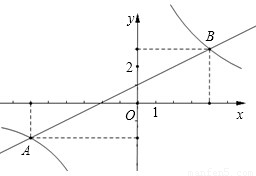 (2008•广州)如图,一次函数y=kx+b的图象与反比例函数y=
(2008•广州)如图,一次函数y=kx+b的图象与反比例函数y=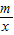 的图象相交于A、B两点.
的图象相交于A、B两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com