
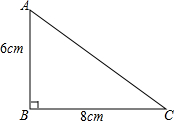
 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度沿AB边向点B移动,以此同时,点Q从点C出发,以2cm/s的速度沿CB边向点B移动,如果P,Q同时出发,经过几秒,△PBQ的面积等于8cm2?
如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm,点P从点A出发,以1cm/s的速度沿AB边向点B移动,以此同时,点Q从点C出发,以2cm/s的速度沿CB边向点B移动,如果P,Q同时出发,经过几秒,△PBQ的面积等于8cm2? 分析 设P、Q同时出发,x秒钟后,AP=xcm,PB=(6-x)cm,BQ=(8-2x)cm,此时△PBQ的面积为:$\frac{1}{2}$×(8-2x)(6-x),令该式=8,由此等量关系列出方程求出符合题意的值.
解答 解:设xs后,可使△PBQ的面积为8cm2.
由题意得,AP=xcm,PB=(6-x)cm,BQ=(8-2x)cm,
则$\frac{1}{2}$(6-x)•(8-2x)=8,
整理,得x2-10x+16=0,
解得x1=2,x2=8(不合题意舍去).
所以P、Q同时出发,2s后可使△PBQ的面积为8cm2.
点评 本题主要考查一元二次方程的应用,关键在于根据三角形面积公式找出等量关系列出方程求解.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:初中数学 来源: 题型:填空题
 如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为2$\sqrt{3}$.
如图,等边△ABC中,BC=6,D、E分别在BC、AC上,且DE∥AC,MN是△BDE的中位线.将线段DE从BD=2处开始向AC平移,当点D与点C重合时停止运动,则在运动过程中线段MN所扫过的区域面积为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
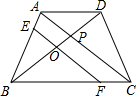 如图,在梯形ABCD中,AD∥BC,BC=2AD,O是BD的中点,过点O作EF∥AC交AB于E,交BC于F,若AC=16cm,求EF的长度.
如图,在梯形ABCD中,AD∥BC,BC=2AD,O是BD的中点,过点O作EF∥AC交AB于E,交BC于F,若AC=16cm,求EF的长度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
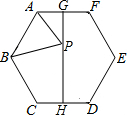 如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )
如图,已知正六边形ABCDEF的边长为2,G,H分别是AF和CD的中点,P是GH上的动点,连接AP,BP,则AP+BP的最小值为( )| A. | 4 | B. | $\sqrt{3}$+2 | C. | $\sqrt{7}$+1 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 进价(元/台) | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 日期 | A款女鞋销量 | B款女鞋销量 | 销售总额 |
| 6月1日 | 12双 | 8双 | 2240元 |
| 6月2日 | 8双 | 10双 | 1960元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com