
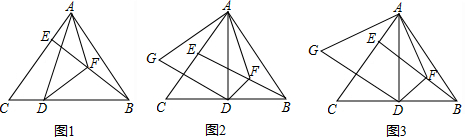
分析 (1)由角平分线得出∠ADF=∠BDF,进而判断出△ADF≌△BDF,即可得出AF=BF即可得出结论;
(2)先判断出∠DAF=∠DBE,再由等角的余角相等得出∠DAF=∠CAD,再由折叠的性质得出∠CAG=∠CAD即可判断出结论;
(3)先判断出,△ADE≌△BDH得出BH=AE=2,DE=DH,进而判断出△DEG≌△DHE得出EH=DG,得出BE=8,最后用勾股定理求出即可.
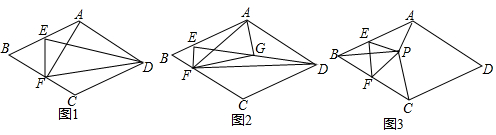
解答 解:(1)∵∠ADB的角平分线DF交BE于点F,
∴∠ADF=∠BDF,
在△ADF和△BDF中,$\left\{\begin{array}{l}{DA=DB}\\{∠ADF=∠BDF}\\{DF=DF}\end{array}\right.$,
∴△ADF≌△BDF,
∴AF=BF,
∴∠FAB=∠FBA;
(2)2∠GAC=∠EAF,
理由:如图2,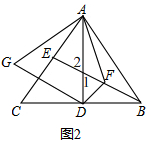
由(1)知,∠FAB=∠FBA,
∵DA=DB,
∴∠DAB=∠DBA,
∴∠DAF=∠DBE,
∵∠ADB=90°,
∴∠DBE+∠1=90°,
∵∠1=∠2,
∴∠DBE+∠2=90°,
∵BE⊥AC,
∴∠CAD+∠2=90°,
∴∠CAD=∠DBE,
∴∠DAF=∠CAD,
由折叠得,∠CAG=∠CAD,
∴∠EAF=∠CAD+∠DAF=2∠CAD=2∠GAC.
(3)如图3,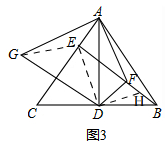
过D作DH⊥DE交EB于H,
∴∠EDH=90°,
∴∠ADE+∠ADH=90°,
∵∠ADH+∠BDH=90°,
∴∠ADE=∠BDH,
在△ADE和△BDH中,$\left\{\begin{array}{l}{∠ADE=∠BDH}\\{AD=DB}\\{∠DAE=∠BDH}\end{array}\right.$,
∴△ADE≌△BDH,
∴BH=AE=2,DE=DH,
∴∠DEH=∠DHE,
由折叠得,EG=ED,∠DGE=∠GDE,DG⊥AC,
∵BE⊥AC,
∴DG∥BE,
∴∠GDE=∠BEH=∠DHE,
在△DEG和△DHE中,$\left\{\begin{array}{l}{∠EGD=∠DEH}\\{∠EDG=∠DHE}\\{DE=DH}\end{array}\right.$,
∴△DEG≌△DHE,
∴EH=DG=6,
∴EB=GD+AE=8,
在Rt△ABE中,AE=2,BE=8,
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=2$\sqrt{17}$.
点评 此题是几何变换综合题,主要考查了全等三角形的性质和判定,角平分线的定义,折叠性质,勾股定理,同角的余角相等,直角三角形的性质,解本题的关键是判断出△ADE≌△BDH.


科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中模拟数学试卷(解析版) 题型:单选题
某工厂现有95个工人,一个工人每天可做8个螺杆或22个螺母,两个螺母和一个螺杆为一套,现在要求工人每天做的螺杆和螺母完整配套而没有剩余,若设安排x个工人做螺杆,y个工人做螺母,则列出正确的二元一次方程组为( )
A. 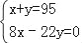 ; B.
; B. 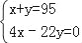 ; C.
; C. 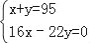 ; D.
; D. 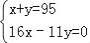
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
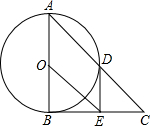 如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.
如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com