
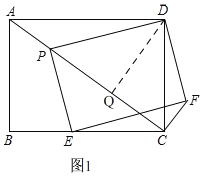
【题目】如图,矩形ABCD中,AB=6,AD=8,P、E分别是线段AC、BC上的点,且四边形PEFD是矩形,若△PCD是等腰三角形,求AP的长.

【答案】AP=4或AP=5或AP=![]()
【解析】试题分析:先求出AC,再分三种情况讨论计算即可得出结论.
试题解析:在矩形ABCD中,AB=6,AD=8,∠ADC=90°,
∴DC=AB=6,
∴AC=![]() =10,
=10,
要使△PCD是等腰三角形,
①当CP=CD时,AP=AC-CP=10-6=4,
②当PD=PC时,∠PDC=∠PCD,
∵∠PCD+∠PAD=∠PDC+∠PDA=90°,
∴∠PAD=∠PDA,
∴PD=PA,
∴PA=PC,
∴AP=![]() AC=5,
AC=5,
③当DP=DC时,如图1,过点D作DQ⊥AC于Q,则PQ=CQ,
∵S△ADC=![]() ADDC=
ADDC=![]() ACDQ,
ACDQ,
∴DQ=![]() ,
,
∴CQ=![]() ,
,
∴PC=2CQ=![]() ,
,
∴AP=AC-PC=10-![]() =
=![]() ;
;
所以,若△PCD是等腰三角形时,AP=4或5或![]() .
.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点E在AD边上,点F在AD的延长线上,且BE=CF.
(1)求证:四边形EBCF是平行四边形.
(2)若∠BEC=90°,∠ABE=30°,AB=![]() ,求ED的长.
,求ED的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干个大小相同,棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:
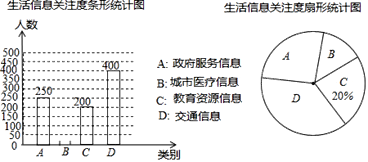
(1)本次参与调查的人数有______ 人;
(2)关注城市医疗信息的有______ 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
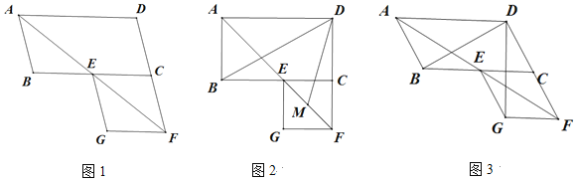
【题目】在平行四边形ABCD中,∠BAD的平分线交线段BC于点E,交线段DC的延长线于点F,以EC、CF为邻边作平行四边形ECFG.
(1)如图1,证明平行四边形ECFG为菱形;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数;
(3)如图3,若∠ABC=120°,请直接写出∠BDG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
例如:方程![]() 的解为
的解为![]() ,不等式组
,不等式组![]() 的解集为
的解集为![]() ,因为
,因为![]() ,所以,称方程
,所以,称方程![]() 为不等式组
为不等式组![]() 的关联方程.
的关联方程.
(1)在方程①![]() ,②
,②![]() ,③
,③![]() 中,不等式组
中,不等式组![]() 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)
(2)若不等式组 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
(3)若方程![]() ,
,![]() 都是关于
都是关于![]() 的不等式组
的不等式组![]() 的关联方程,求
的关联方程,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4 ![]() ,则图中阴影部分的面积为( )
,则图中阴影部分的面积为( ) 
A.π+1
B.π+2
C.2π+2
D.4π+1
查看答案和解析>>
科目:初中数学 来源: 题型:
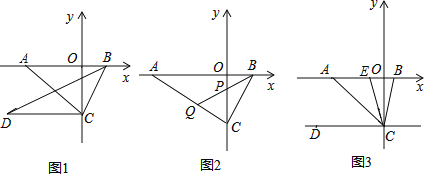
【题目】如图1,在平面直角坐标系中,点A为x轴负半轴上一点,点B为x轴正半轴上一点,![]() ,
,![]() ,其中a、b满足关系式:
,其中a、b满足关系式:![]() .
.
![]() ______,
______,![]() ______,
______,![]() 的面积为______;
的面积为______;
![]() 如图2,石
如图2,石![]() 于点C,点P是线段OC上一点,连接BP,延长BP交AC于点
于点C,点P是线段OC上一点,连接BP,延长BP交AC于点![]() 当
当![]() 时,求证:BP平分
时,求证:BP平分![]() ;
;![]() 提示:三角形三个内角和等于
提示:三角形三个内角和等于![]()
![]() 如图3,若
如图3,若![]() ,点E是点A与点B之间上一点连接CE,且CB平分
,点E是点A与点B之间上一点连接CE,且CB平分![]() 问
问![]() 与
与![]() 有什么数量关系?请写出它们之间的数量关系并请说明理由.
有什么数量关系?请写出它们之间的数量关系并请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com