
【题目】如图,在四边形ABCD中,∠ABC=∠BCD=90°,点E为BC的中点,AE⊥DE.
(1)求证:△ABE∽△ECD;
(2)求证:AE2=AB·AD;
(3)若AB=1,CD=4,求线段AD,DE的长.

【答案】(1)证明见解析;(2)证明见解析;(3)10.
【解析】试题分析:(1)根据垂直的定义和直角三角形的性质,求出∠BAE=∠CED,然后利用两角对应相等的两三角形相似可证;
(2)根据相似三角形的性质:相似三角形的对应边成比例,以及两边对应成比例且夹角相等的两三角形相似,可证明结论;
(3)根据相似三角形的性质,由(2)的结论△ABE∽△AED得到对应边成比例,然后根据勾股定理求解.
试题解析:(1)证明:∵AE⊥DE,∴∠AED=90°,∴∠AEB+∠CED=180°-90°=90°,
∵∠ABC=90°,∴∠BAE+∠AEB=90°,∴∠BAE=∠CED.
又∵∠ABC=∠BCD,∴△ABE∽△ECD.
(2) ∵△ABE∽△ECD,∴ ![]() .
.
∵点E为BC的中点,∴BE=EC.
∴![]() .
.
又∵∠ABC=∠AED=90°,∴△ABE∽△AED,
∴![]() ,∴AE2=AB·AD.
,∴AE2=AB·AD.
(3)∵△ABE∽△ECD,∴ ![]() .
.
∵AB=1,CD=4,BE=EC,∴BE2=AB·CD=4.
由勾股定理,得AE2=AB2+ BE2=5.
∵AE2=AB·AD,∴![]() .
.
由勾股定理,得![]() .
.


科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣5)﹣(+3)+(﹣9)﹣(﹣7)
(2)(+5![]() )+(﹣3
)+(﹣3![]() )+(﹣6
)+(﹣6![]() )+(﹣15
)+(﹣15![]() )
)
(3)|﹣6![]() |+(﹣8)+|﹣3﹣
|+(﹣8)+|﹣3﹣![]() |
|
(4)78×(﹣![]() )+(﹣11)×(﹣
)+(﹣11)×(﹣![]() )+(﹣33)×0.6
)+(﹣33)×0.6
(5)(﹣2)2010×(﹣0.5)2009+(﹣6![]() )×7
)×7
(6)﹣14﹣![]() ×[2﹣(﹣3)﹣2]
×[2﹣(﹣3)﹣2]
查看答案和解析>>
科目:初中数学 来源: 题型:
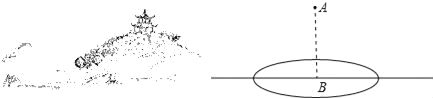
【题目】如图,湖心岛上有一凉亭,现欲利用湖岸边的开阔平整地带,测量凉亭顶端到湖面所在平面的高度AB(见示意图),可供使用的工具有测倾器、皮尺.
(1)请你根据现有条件,设计一个测量凉亭顶端到湖面所在平面的高度AB的方案,画出测量方案的平面示意图,并将测量的数据标注在图形上(所测的距离用m,n,…表示,角用α,β,…表示,测倾器高度忽略不计);
(2)根据你所测量的数据,计算凉亭到湖面的高度AB(用字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应学习任务:
四点共圆的条件
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?小明经过实践探究发现:过对角互补的四边形的四个顶点能作一个圆,下面是小明运用反证法证明上述命题的过程:
已知:在四边形ABCD中,∠B+∠D=180°.
求证:过点A、B、C、D可作一个圆.
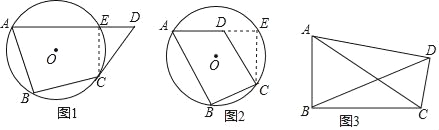
证明:如图(1),假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆外,设AD与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠D=180°,所以∠AEC=∠D,而∠AEC是△CED的外角,∠AEC>∠D,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
如图(2)假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆内,设AD的延长线与圆相交于点E,连接CE,则∠B+∠AEC=180°,而已知∠B+∠ADC=180°,所以∠AEC=∠ADC,而∠ADC是△CED的外角,∠ADC>∠AEC,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
因此得到四点共圆的条件:过对角互补的四边形的四个顶点能作一个圆.
学习任务:
(1)材料中划线部分结论的依据是 .
(2)证明过程中主要体现了下列哪种数学思想: (填字母代号即可)
A、函数思想 B、方程思想 C、数形结合思想 D、分类讨论思想
(3)如图(3),在四边形ABCD中,∠ABC=∠ADC=90°,∠CAD=16°.AD=BD,则求∠ADB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E是射线BC上的点,直线AF与直线AB关于直线AE对称,直线AF交射线CD于点F.
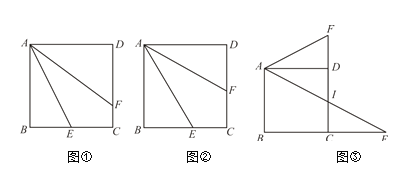
(1)如图①,当点E是线段BC的中点时,求证:AF=AB+CF;
(2)如图②,当∠BAE=30°时,求证:AF=2AB﹣2CF;
(3)如图③,当∠BAE=60°时,(2)中的结论是否还成立?若不成立,请判断AF与AB、CF之间的数量关系,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,BD是中线,延长BC至E,CE=CD,

(1)求证:DB=DE
(2)在图中过D作DF⊥BE交BE于F,若CF=4,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com