
【题目】某市规定了每月用水![]() 立方米以内(含
立方米以内(含![]() 立方米)和用水
立方米)和用水![]() 立方米以上两种不同的收费标准.该市的用户每月应交水费
立方米以上两种不同的收费标准.该市的用户每月应交水费![]() (元)是用水量
(元)是用水量![]() (立方米)的函数,其图象如图所示.
(立方米)的函数,其图象如图所示.
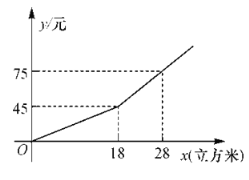
(1)若每月用水量为![]() 立方米,则应交水费多少元?.
立方米,则应交水费多少元?.
(2)求当![]() 时,
时,![]() 关于
关于![]() 的函数解析式.
的函数解析式.
(3)若小敏家某月交水费![]() 元,则这个月用水量为多少立方米?
元,则这个月用水量为多少立方米?
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】教材原题解答:
已知![]() 是含字母
是含字母![]() 的单项式,要使多项式
的单项式,要使多项式![]() 是某个多项式的平方,求
是某个多项式的平方,求![]() .
.
解:根据完全平方公式,分两种情况:
当![]() 为含字母
为含字母![]() 的一次单项式时,
的一次单项式时,
![]()
![]() .
.
当![]() 为含字母
为含字母![]() 的四次单项式时,
的四次单项式时,
则![]()
![]() 为
为![]() 或
或![]() 或
或![]()
问题发现:
由上面问题解答过程,我们可以得到下列等式:
![]() .
.
观察等式的左边多项式的系数发现:![]() .
.
爱学习的小明又进行了很多运算:![]() 等等,
等等,
发现同样有![]() .
.
于是小明猜测:若多项式![]() (
(![]() 是常数,
是常数,![]() )是某个含
)是某个含![]() 的多项式的平方,则系数
的多项式的平方,则系数![]() 一定存在某种关系
一定存在某种关系
问题解决:
(1)请用代数式表示![]() 之间的关系;
之间的关系;
(2)若多项式![]() 加上一个含字母y的单项式,就能变形为一个含
加上一个含字母y的单项式,就能变形为一个含![]() 的多项式的平方,请直接写出所有满足条件的单项式,
的多项式的平方,请直接写出所有满足条件的单项式,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在坡角为30°的山坡上有一竖立的旗杆AB,其正前方矗立一墙,当阳光与水平线成45°角时,测得旗杆AB落在坡上的影子BD的长为8米,落在墙上的影子CD的长为6米,求旗杆AB的高(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把三角形纸片![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在四边形
落在四边形![]() 内部点
内部点![]() 处,
处,
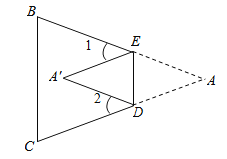
(1)写出图中一对全等的三角形,井写出它们的所有对应角.
(2)设![]() 的度数为
的度数为![]() ,
,![]() 的度数为
的度数为![]() ,那么
,那么![]() 的度数分别是多少(用含
的度数分别是多少(用含![]() 或
或![]() 的式子表示)?
的式子表示)?
(3)![]() 与
与![]() 之间有一种数量关系始终保持不变,请找出这个规律,井说明理由.
之间有一种数量关系始终保持不变,请找出这个规律,井说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂要把一批产品从A地运往B地,若通过铁路运输,则每千米需交运费15元,还要交装卸费400元及手续费200元,若通过公路运输,则每千米需要交运费25元,还需交手续费100元(由于本厂职工装卸,不需交装卸费).设A地到B地的路程为x km,通过铁路运输和通过公路运输需交总运费y1元和y2元,
(1)求y1和y2关于x的表达式.
(2)若A地到B地的路程为120km,哪种运输可以节省总运费?
查看答案和解析>>
科目:初中数学 来源: 题型:
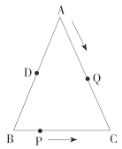
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,如果点
的中点,如果点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向点
向点![]() 移动,同时点
移动,同时点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 以
以![]() 的速度移动,若
的速度移动,若![]() 、
、![]() 同时出发,当有一个点移动到点
同时出发,当有一个点移动到点![]() 时,
时,![]() 、
、![]() 都停止运动,设
都停止运动,设![]() 、
、![]() 移动时间为
移动时间为![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)当![]() 时,问
时,问![]() 与
与![]() 是否全等,并说明理由.
是否全等,并说明理由.
(3)![]() 时,若
时,若![]() 为等腰三角形,求
为等腰三角形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(
经过点A(![]() ,0),B(
,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com