
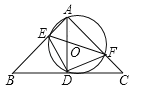
【题目】如图,在![]() 中,
中,![]()
![]()
![]() ,垂足为
,垂足为![]() ,过
,过![]() 的⊙O分别与
的⊙O分别与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ≌
≌![]() ;
;
(2)当![]() 与⊙O相切时,求⊙O的面积.
与⊙O相切时,求⊙O的面积.
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)由等腰直角三角形的性质知AD=CD、∠1=∠C=45°,由∠EAF=90°知EF是⊙O的直径,据此知∠2+∠4=∠3+∠4=90°,得∠2=∠3,利用“ASA”证明即可得;
(2)当BC与⊙O相切时,AD是直径,根据∠C=45°、AC=![]() 可得AD=1,利用圆的面积公式可得答案.
可得AD=1,利用圆的面积公式可得答案.
详解:(1)如图,∵AB=AC,∠BAC=90°,∴∠C=45°.
又∵AD⊥BC,AB=AC,∴∠1=![]() ∠BAC=45°,BD=CD,∠ADC=90°.
∠BAC=45°,BD=CD,∠ADC=90°.
又∵∠BAC=90°,BD=CD,∴AD=CD.
又∵∠EAF=90°,∴EF是⊙O的直径,∴∠EDF=90°,∴∠2+∠4=90°.
又∵∠3+∠4=90°,∴∠2=∠3.在△ADE和△CDF中.
∵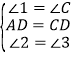 ,∴△ADE≌△CDF(ASA).
,∴△ADE≌△CDF(ASA).
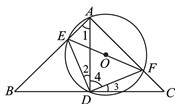
(2)当BC与⊙O相切时,AD是直径.在Rt△ADC中,∠C=45°,AC=![]() ,∴sin∠C=
,∴sin∠C=![]() ,∴AD=ACsin∠C=1,∴⊙O的半径为
,∴AD=ACsin∠C=1,∴⊙O的半径为![]() ,∴⊙O的面积为
,∴⊙O的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】综合与探究
问题情境:
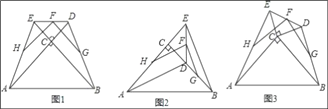
(1)如图1,两块等腰直角三角板△ABC和△ECD如图所示摆放,其中∠ACB=∠DCE=90°,点F,H,G分别是线段DE,AE,BD的中点,A,C,D和B,C,E分别共线,则FH和FG的数量关系是 ,位置关系是 .
合作探究:
(2)如图2,若将图1中的△DEC绕着点C顺时针旋转至A,C,E在一条直线上,其余条件不变,那么(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,若将图1中的△DEC绕着点C顺时针旋转一个锐角,那么(1)中的结论是否还成立?若成立,请证明,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
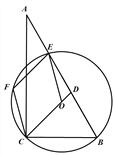
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,经过B,C两点的⊙O交边AB于另一点E,延长CO交边AB于点D,EF∥CD交⊙O于另一点F, 连接CF。
(1)若⊙O的半径为4,求弧CE的长;
(2)求证:四边形EFCO是菱形;
(3)若BC=6,tan∠CDB=3,求BD的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 阅读材料:
为落实水资源管理制度,大力促进水资源节约,本市居民用水实行阶梯水价,按年度用水量计算,将居民家庭全年用水量划分为三档,水价分档递增,实施细则如表:

如某户居民去年用水量为190立方米,则其应缴纳水费为180×5+(190﹣180)×7=970元.
(1)若小明家去年用水量为100立方米,则小明家应缴纳的水费为________元;
(2)若截止10月底,小明家今年共纳水费1145元,则小明家共用水_______立方米;
(3)若小明家全年用水量x不超过270立方米,则应缴纳的水费为多少元?(用含x的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )

A.  B.
B. 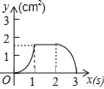 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在公路上行驶,看到里程表上是一个两位数,1小时后其里程表还是一个两位数,且刚好它的十位数字与个位数字与第一次看到的两位数的十位数字与个位数字颠倒了位置,又过了1小时后看到里程表是一个三位数,它是第一次看到的两位数中间加一个0,则汽车的速度是( )千米/小时.
A. 35B. 40C. 45D. 50
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举行“汉字听写”比赛,每名学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.

组别 | 正确字数 | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 25 |
D |
| m |
E |
| n |
根据以上信息解决下列问题:
(1)在统计表中,![]() ______,
______,![]() ______;
______;
(2)请补全频数分布直方图.
(3)扇形统计图中“C”对应扇形的圆心角的度数是_______.
(4)若该校共有1200名学生参加此次“汉字听写”比赛,估计此次参加比赛听写正确字数不低于24个的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com