Question

在半径为6cm的圆中，内接正三角形的边长为

 

cm，边心距为

 

cm．

Answer 1

分析：作出几何图形，在由外接圆半径、边心距和边长的一半组成的三角形中，已知外接圆半径和特殊角，可求得边心距，进而边长的一半，可解．

解答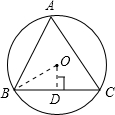：解：如图，△ABC是⊙O的内接等边三角形，OB=6cm，OD⊥BC．
等边三角形的内心和外心重合，所以OB平分∠ABC，则∠OBD=30°；
∵OD⊥BC，
∴BD=DC，
又∵OB=6，
∴OD=3，BD=3

3

cm，则BC=6

3

cm．
故填6

3

；3．

点评：熟练掌握等边三角形的性质．注意：等边三角形的外接圆和内切圆是同心圆，圆心到顶点的距离等于外接圆半径，边心距等于内切圆半径．