
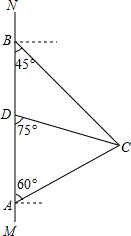
 如图,在南北方向的海岸线MN上,有A,B两艘巡逻船,现均收到故障船C的求救信号,已知A,B两船相距100($\sqrt{3}$+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
如图,在南北方向的海岸线MN上,有A,B两艘巡逻船,现均收到故障船C的求救信号,已知A,B两船相距100($\sqrt{3}$+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.分析 (1)作CE⊥AB于E,设AB=x海里,根据正切的概念求出CE,根据题意列方程,解方程即可;
(2)作DF⊥AC于F,设AF=y,用y表示出DF,根据题意列方程,解方程即可.
解答 解:(1)作CE⊥AB于E,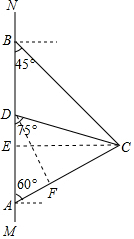
设AB=x海里,
在Rt△AEC中,CE=AE×tan∠EAC=$\sqrt{3}$x,
在Rt△BEC中,∠EBC=45°,
∴BE=EC=$\sqrt{3}$x,
则x+$\sqrt{3}$x=100($\sqrt{3}$+1),
解得,x=100,
∵∠ACE=30°,
∴AC=2x=200,
答:A与C之间的距离AC为200海里;
(2)作DF⊥AC于F,
设AF=y,则DF=$\sqrt{3}$y,
∵∠DAC=60°,∠ADC=75°,
∴∠DCA=45°,
∴CF=DF=$\sqrt{3}$y,
则y+$\sqrt{3}$y=200,
解得,y=100($\sqrt{3}$-1),
∴DF=$\sqrt{3}×$100($\sqrt{3}$-1)≈127,
∵127>100,
∴巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的定义、正确标注方向角是解题的关键.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
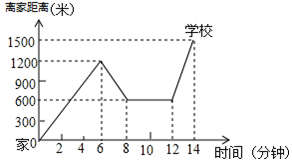 “珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com