
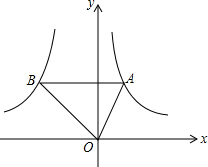
 如图,点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象于点B,且S△AOB=5.
如图,点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,过点A作AB∥x轴,交另一个反比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象于点B,且S△AOB=5.分析 (1)首先设AB交y轴于点C,由点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,AB∥x轴,根据反比例函数系数k的几何意义求得△AOC的面积,又由△AOB的面积等于5,可求得△BOC的面积,继而求得k的值;
(2)①由点A的横坐标是1,可求得点A的坐标,继而求得点B的纵坐标,则可求得点B的坐标,则可求得AB,OA,OB的长,然后由勾股定理的逆定理,求得∠AOB的度数;
②过点A作AM⊥x轴于点A,过点P作PN⊥x轴于点N,设P(x,-$\frac{8}{x}$),根据反比例函数系数k的几何意义得出S△NOP=$\frac{1}{2}$×8=4,S△AOM=$\frac{1}{2}$×2=1.由S△AOP=S△梯形APNM-S△NOP-S△AOM=S△AOB=5,列出方程$\frac{1}{2}$(2-$\frac{8}{x}$)×(1-x)-4-1=5,解方程即可.
解答 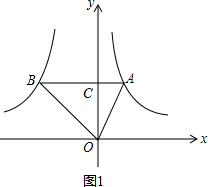 解:(1)如图1,设AB交y轴于点C,
解:(1)如图1,设AB交y轴于点C,
∵点A是反比例函数y1=$\frac{2}{x}$(x>0)图象上的任意一点,且AB∥x轴,
∴AB⊥y轴,
∴S△AOC=$\frac{1}{2}$×2=1,
∵S△AOB=5,
∴S△BOC=4,
∵反比例函数y2=$\frac{k}{x}$(k<0,x<0)的图象过点B,AB⊥y轴,
∴-$\frac{1}{2}$k=4,
∴k=-8;
故答案为:-8;
(2)①∵点A的横坐标是1,
∴y=$\frac{2}{1}$=2,
∴点A(1,2),
∵AB∥x轴,
∴点B的纵坐标为2,
∴2=-$\frac{8}{x}$,
解得:x=-4,
∴点B(-4,2),
∴AB=AC+BC=1+4=5,OA=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,OB=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴OA2+OB2=AB2,
∴∠AOB=90°;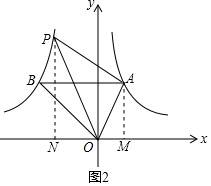
②如图2,过点A作AM⊥x轴于点A,过点P作PN⊥x轴于点N,设P(x,-$\frac{8}{x}$),
则S△NOP=$\frac{1}{2}$×8=4,S△AOM=$\frac{1}{2}$×2=1.
∵S△AOP=S△梯形APNM-S△NOP-S△AOM=S△AOB=5,
∴$\frac{1}{2}$(2-$\frac{8}{x}$)×(1-x)-4-1=5,
整理,得x2+5x+4=0,
解得x1=-1,x2=-4(不合题意舍去),
∴点P的坐标为(-1,8).
点评 此题考查了反比例函数的系数k的几何意义,反比例函数图象上点的坐标特征,勾股定理的逆定理,图形的面积等知识.注意第(2)问②中,设P(x,-$\frac{8}{x}$),根据S△AOP=S△梯形APNM-S△NOP-S△AOM=S△AOB=5列出方程是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
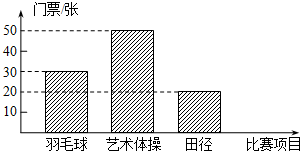 2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.
2010年5月20日上午10时起.2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分价格,如图为某公司购买的门票种类、数量所绘制的条形统计图.| 比赛项目 | 票价(元/张) |
| 羽毛球 | 400 |
| 艺术体操 | 240 |
| 田径 | x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com