
【题目】已知△ABC的三边a,b,c中,a=b-1,c=b+1,又已知关于x的方程4x2-20x+b+12=0的根恰为b的值,求△ABC的面积.
【答案】6.
【解析】【试题分析】根据方程的根的定义,将x=b代入原方程,整理得4b2-19b+12=0,解得b1=4,b2=![]() .根据b的取值,分类讨论,当b1=4时,a=3,c=5,根据勾股定理的逆定理得:△ABC为直角三角形,且∠C=90°.得:S△ABC=
.根据b的取值,分类讨论,当b1=4时,a=3,c=5,根据勾股定理的逆定理得:△ABC为直角三角形,且∠C=90°.得:S△ABC=![]() ab=
ab=![]() ×3×4=6;当b2=
×3×4=6;当b2=![]() 时,a=
时,a=![]() -1<0,不符合题意,舍去.
-1<0,不符合题意,舍去.
【试题解析】
将x=b代入原方程,整理得4b2-19b+12=0,解得b1=4,b2=![]() .当b1=4时,a=3,c=5,∵32+42=52,即a2+b2=c2,∴△ABC为直角三角形,且∠C=90°.∴S△ABC=
.当b1=4时,a=3,c=5,∵32+42=52,即a2+b2=c2,∴△ABC为直角三角形,且∠C=90°.∴S△ABC=![]() ab=
ab=![]() ×3×4=6;当b2=
×3×4=6;当b2=![]() 时,a=
时,a=![]() -1<0,不合题意,舍去.因此,△ABC的面积为6.
-1<0,不合题意,舍去.因此,△ABC的面积为6.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
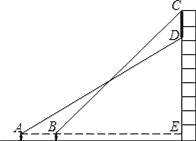
【题目】如图所示,小杨在广场上的A处正面观测一座楼房墙上的广告屏幕,测得屏幕下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该屏幕上端C处的仰角为45°.若该楼高为26.65m,小杨的眼睛离地面1.65m,广告屏幕的上端与楼房的顶端平齐.求广告屏幕上端与下端之间的距离.(![]() ≈1.732,结果精确到0.1m)
≈1.732,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC的平分线交AC于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同庆中学为丰富学生的校园生活,准备从军跃体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据同庆中学的实际情况,需从军跃体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1+∠2=180°,∠3=∠B,试判断∠AED与∠C的大小关系,并证明你的结论. 
解:∠C与∠AED相等,理由如下:
∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义)
∴∠2= . ( . ),
∴AB∥EF( . )
∴∠3= . ( . )
又∠B=∠3(已知)
∴∠B= . (等量代换)
∴DE∥BC( . )
∴∠C=∠AED( . ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com