
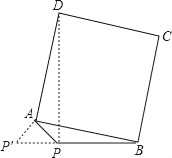
【题目】已知:PA=![]() ,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
,PB=4,以AB为一边作正方形ABCD,使P、D两点落在直线AB的两侧.
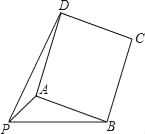
(1)如图,当∠APB=45°时,求AB及PD的长;
(2)当∠APB变化,且其它条件不变时,求PD的最大值,及相应∠APB的大小.
【答案】
【1】(1)①如图11,作AE⊥PB于点E.
∵△APE中,∠APE=45°,![]() ,
,
∴![]() ,
,
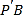
![]() .
.
∵![]() ,
,
∴![]() .
.
在Rt△ABE中,∠AEB=90°,
∴![]() .…………1分
.…………1分
②解法一:如图12,因为四边形ABCD为正方形,可将
△PAD绕点A顺时针旋转90°得到△![]() ,
,
可得△![]() ≌△
≌△![]() ,
,![]() ,
,![]() .
.
∴![]() =90°,
=90°,![]() =45°,
=45°,![]() =90°.
=90°.
∴![]() .分
.分
∴![]() .…………2分
.…………2分
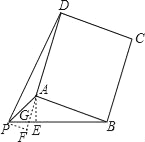 解法二:如图13,过点P作AB的平行线,与DA的延长线交于F,设DA的 延长线交PB于G.
解法二:如图13,过点P作AB的平行线,与DA的延长线交于F,设DA的 延长线交PB于G.
在Rt△AEG中,可得
![]() ,
,
![]() ,
,![]() .
.
在Rt△PFG中,可得![]() ,
,![]() .
.
在Rt△PDF中,可得![]()
![]() .
.
【2】(2)如图14所示,将△PAD绕点A顺时针旋转90°得到△![]() , PD 的最大值即为
, PD 的最大值即为![]() 的最大值.
的最大值.
∵△![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
且P、D两点落在直线AB的两侧,
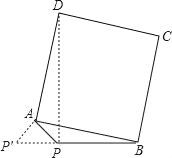
∴当![]() 三点共线时,
三点共线时,![]() 取得最大值(见图15).
取得最大值(见图15).
此时![]() ,即
,即![]() 的最大值为6. …………4分
的最大值为6. …………4分
 此时∠APB=180°-
此时∠APB=180°-![]() =135°. …………5分
=135°. …………5分
【解析】
(1)作辅助线,过点A作AE⊥PB于点E,在Rt△PAE中,已知∠APE,AP的值,根据三角函数可将AE,PE的值求出,由PB的值,可求BE的值,在Rt△ABE中,根据勾股定理可将AB的值求出;
求PD的值有两种解法,解法一:可将△PAD绕点A顺时针旋转90°得到△P'AB,可得△PAD≌△P'AB,求PD长即为求P′B的长,在Rt△AP′P中,可将PP′的值求出,在Rt△PP′B中,根据勾股定理可将P′B的值求出;
解法二:过点P作AB的平行线,与DA的延长线交于F,交PB于G,在Rt△AEG中,可求出AG,EG的长,进而可知PG的值,在Rt△PFG中,可求出PF,在Rt△PDF中,根据勾股定理可将PD的值求出;
(2)将△PAD绕点A顺时针旋转90°,得到△P'AB,PD的最大值即为P'B的最大值,故当P'、P、B三点共线时,P'B取得最大值,根据P'B=PP'+PB可求P'B的最大值,此时∠APB=180°-∠APP'=135°.
(1)①
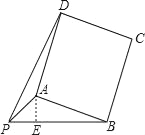
如图,作AE⊥PB于点E,
∵△APE中,∠APE=45°,PA=![]() ,
,
∴AE=PE=![]() ×
×![]() =1,
=1,
∵PB=4,∴span>BE=PB﹣PE=3,
在Rt△ABE中,∠AEB=90°,
∴AB=![]() =
=![]() .
.
②解法一:
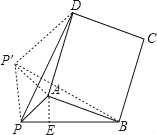
如图,因为四边形ABCD为正方形,可将
△PAD绕点A顺时针旋转90°得到△P'AB,
可得△PAD≌△P'AB,PD=P'B,PA=P'A.
∴∠PAP'=90°,∠APP'=45°,∠P'PB=90°
∴PP′=![]() PA=2,
PA=2,
∴PD=P′B=![]() =
=![]() =
=![]() ;
;
解法二:
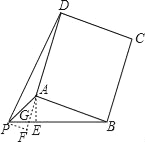
如图,过点P作AB的平行线,与DA的延长线交于F,与DA的
延长线交PB于G.
在Rt△AEG中,
可得AG=![]() =
=![]() =
=![]() ,EG=
,EG=![]() ,PG=PE﹣EG=
,PG=PE﹣EG=![]() .
.
在Rt△PFG中,
可得PF=PGcos∠FPG=PGcos∠ABE=![]() ,FG=
,FG=![]() .
.
在Rt△PDF中,可得,
PD=![]() =
=![]() =
=![]() .
.
(2)如图所示,
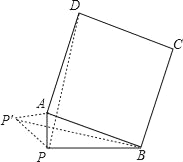
将△PAD绕点A顺时针旋转90°
得到△P'AB,PD的最大值即为P'B的最大值,
∵△P'PB中,P'B<PP'+PB,PP′=![]() PA=2,PB=4,
PA=2,PB=4,
且P、D两点落在直线AB的两侧,
∴当P'、P、B三点共线时,P'B取得最大值(如图)
此时P'B=PP'+PB=6,即P'B的最大值为6.
此时∠APB=180°﹣∠APP'=135度.
考查综合应用解直角三角形、直角三角形性质,进行逻辑推理能力和运算能力,在解题过程中通过添加辅助线,确定P′B取得最大值时点P′的位置.


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
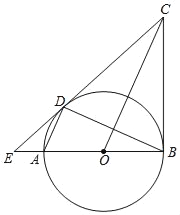
【题目】如图,已知AB为⊙O的直径,AD,BD是⊙O的弦,BC是⊙O的切线,切点为B,OC∥AD,BA,CD的延长线相交于点E.
(1)求证:DC是⊙O的切线;
(2)若⊙O半径为4,∠OCE=30°,求△OCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(m-2)x2+(m+3)x+m+2的图象过点(0,5)
(1)求m的值,并写出二次函数的表达式;
(2)求出二次函数图象的顶点坐标、对称轴。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次羽毛球赛中,甲运动员在离地面![]() 米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0).
米的P点处发球,球的运动轨迹PAN看作一个抛物线的一部分,当球运动到最高点A时,其高度为3米,离甲运动员站立地点O的水平距离为5米,球网BC离点O的水平距离为6米,以点O为原点建立如图所示的坐标系,乙运动员站立地点M的坐标为(m,0).

(1)求抛物线的解析式(不要求写自变量的取值范围);
(2)求羽毛球落地点N离球网的水平距离(即NC的长);
(3)乙原地起跳后可接球的最大高度为2.4米,若乙因为接球高度不够而失球,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=90°,AB=AD,CB=CD,一个以点C为顶点的45°角绕点C旋转,角的两边与BA,DA交于点M,N,与BA,DA的延长线交于点E,F,连接AC.
(1)在∠FCE旋转的过程中,当∠FCA=∠ECA时,如图1,求证:AE=AF;
(2)在∠FCE旋转的过程中,当∠FCA≠∠ECA时,如图2,如果∠B=30°,CB=2,用等式表示线段AE,AF之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
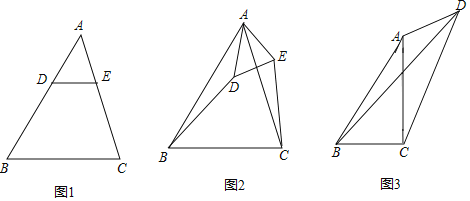
【题目】(1)如图1,在△ABC中,AB>AC,点D,E分别在边AB,AC上,且DE∥BC,若AD=2,AE=![]() ,则
,则![]() 的值是 ;
的值是 ;
(2)如图2,在(1)的条件下,将△ADE绕点A逆时针方向旋转一定的角度,连接CE和BD,![]() 的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
的值变化吗?若变化,请说明理由;若不变化,请求出不变的值;
(3)如图3,在四边形ABCD中,AC⊥BC于点C,∠BAC=∠ADC=θ,且tanθ=![]() ,当CD=6,AD=3时,请直接写出线段BD的长度.
,当CD=6,AD=3时,请直接写出线段BD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
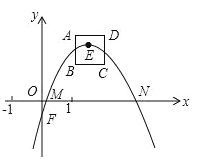
【题目】如图,抛物线l:y=﹣x2+bx+c(b,c为常数),其顶点E在正方形ABCD内或边上,已知点A(1,2),B(1,1),C(2,1).
(1)直接写出点D的坐标_____________;
(2)若l经过点B,C,求l的解析式;
(3)设l与x轴交于点M,N,当l的顶点E与点D重合时,求线段MN的值;当顶点E在正方形ABCD内或边上时,直接写出线段MN的取值范围;
(4)若l经过正方形ABCD的两个顶点,直接写出所有符合条件的c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨举办首届《诗词大会》,九年级2班的马小梅晋级总决赛,比赛过程分两个环节,参赛选手须在每个环节中各选择一道题目.
第一环节:横扫千军、你说我猜、初级飞花令,(分别用![]() )表示;
)表示;
第二环节:出口成诗、飞花令、超级飞花令、诗词接龙(分别用![]() 表示).
表示).
(1)请用画树状图或列表的方法表示马小梅参加总决赛抽取题目的所有可能结果;
(2)求马小梅参加总决赛抽取题目都是飞花令题目(初级飞花令、飞花令、超级飞花令)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com