
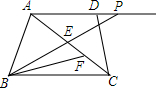
 已知,如图,在梯形ABCD中,AD∥BC,BC=6,点P是射线AD上的点,BP交AC于点E,∠CBP的角平分线交AC于点F,且CF=$\frac{1}{3}$AC时.求AP+BP的值.
已知,如图,在梯形ABCD中,AD∥BC,BC=6,点P是射线AD上的点,BP交AC于点E,∠CBP的角平分线交AC于点F,且CF=$\frac{1}{3}$AC时.求AP+BP的值. 分析 延长BF交射线AP于M,根据AD∥BC,根据两直线平行,内错角相等可得∠M=∠CBM,再根据角平分线的定义可得∠PBM=∠CBM,从而得到∠M=∠PBM,根据等角对等边可得BP=PM,求出AP+BP=AM,再根据AC=$\frac{1}{3}$CF求出AE=2CF,然后根据△MAF和△BCF相似,利用相似三角形对应边成比例列式求解即可.
解答  解:如图,延长BF交射线AP于M,
解:如图,延长BF交射线AP于M,
∵AD∥BC,
∴∠M=∠CBM,
∵BF是∠CBP的平分线,
∴∠PBM=∠CBM,
∴∠M=∠PBM,
∴BP=PM,
∴AP+BP=AP+PM=AM,
∵CF=$\frac{1}{3}$AC,则AF=2CF,
由AD∥BC得,△MAF∽△BCF,
∴$\frac{AM}{BC}=\frac{AF}{CF}$=2,
∴AM=2BC=2×6=12,
即AP+BP=12.
点评 本题考查了相似三角形的判定与性质,角平分线的定义,平行线的性质,延长BF构造出相似三角形,求出AP+BP=AM并得到相似三角形是解题的关键,也是本题的难点.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,OA、OB是两条相交的高速公路,C、D是两处村庄,某百货集团响应新农村建设的要求,要在高速路内建一座大型便民超市P,使PC=PD,且P到∠AOB的两边OA、OB的距离相等,那么超市P的位置应选在哪里?
如图所示,OA、OB是两条相交的高速公路,C、D是两处村庄,某百货集团响应新农村建设的要求,要在高速路内建一座大型便民超市P,使PC=PD,且P到∠AOB的两边OA、OB的距离相等,那么超市P的位置应选在哪里?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
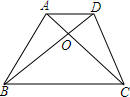 如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且AD:BC=1:2,则下列结论中,错误的是( )
如图,在梯形ABCD中,AD∥BC,对角线AC、BD相交于点O,且AD:BC=1:2,则下列结论中,错误的是( )| A. | S△ABC=S△DBC | B. | S△AOB=S△COD | C. | 2S△AOD=S△BOC | D. | 2S△AOB=S△BOC |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
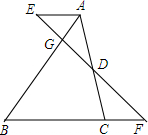 如图,在△ABC中,D是AC的中点,AE∥BC,DE交AB于点G,交BC的延长线于点F,若BG:AG=3:1,BC=10,则线段AE的长为( )
如图,在△ABC中,D是AC的中点,AE∥BC,DE交AB于点G,交BC的延长线于点F,若BG:AG=3:1,BC=10,则线段AE的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
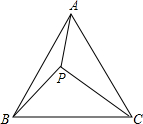 数学探究课上老师处这样一道题:“如图,等边△ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断
数学探究课上老师处这样一道题:“如图,等边△ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军探讨时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路,请按照下列思路要求画图或判断查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com