
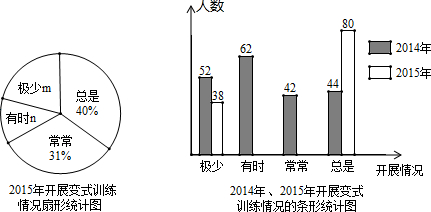
分析 (1)根据总是的人数和所占的百分比求出总人数,再用2015年极少的人数除以总人数即可求出m,再用100%减去其它所占的百分比求出n;最后用360乘以总是所占的百分比即可得出“总是”对应扇形统计图的圆心角的度数;
(2)用总人数乘以“有时”和“常常”所占的百分比即可得出2015年“有时”和“常常”的人数,从而补全统计图;
(3)用该校2015年的总人数乘以“总是”所占的百分比即可得出答案;
(4)与2014年相比,2015年该校开展变式训练的情况有很大的提高.
解答 解:(1)调查的总人数是:$\frac{80}{40%}$=200(人),
则m=$\frac{38}{200}$×100%=19%;n=100%-31%-40%-19%=10%;
“总是”对应扇形统计图的圆心角的度数为:360×40%=144°;
故答案为:m=19%,n=10%,144°;
(2)“有时”的人数是:200×10%=20人,“常常”的人数是:200×31%=62人;
补图如下: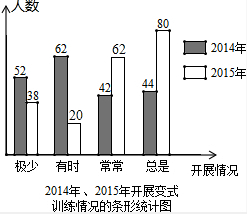
(3)根据题意得:1200×40%=480,
答:其中认为数学课“总是”开展变式训练的学生有480人;
(4)与2014年相比,2015年该校开展变式训练的情况有很大的提高.
点评 本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.
如图,在△ABC和△DCB中,AB=DC,AC=DB,AC与DB交于点M.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
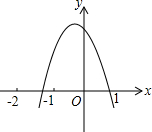 如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )
如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 边长为1的正方形ABCD在平面直角坐标系中位置如图所示,以对角线BD为边作正方形BC1D1D,再以对角线BD1为边作正方形BB1C2D1,再以对角线B1D1为边作正方形B1C3D2D1,…按此规律做第10次所得正方形的顶点C10的坐标为(63,32).
边长为1的正方形ABCD在平面直角坐标系中位置如图所示,以对角线BD为边作正方形BC1D1D,再以对角线BD1为边作正方形BB1C2D1,再以对角线B1D1为边作正方形B1C3D2D1,…按此规律做第10次所得正方形的顶点C10的坐标为(63,32).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
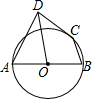 如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D,若BC=$\sqrt{5}$,CD=2,则tan∠ADO的值为( )| A. | $\frac{8}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com