
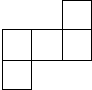
 如图是由五个边长为1的正方形组成的图象,如果把它们剪拼成一个正方形,那么所拼成的正方形边长的平方是多少?边长是有理数吗?请画出示意图.
如图是由五个边长为1的正方形组成的图象,如果把它们剪拼成一个正方形,那么所拼成的正方形边长的平方是多少?边长是有理数吗?请画出示意图. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
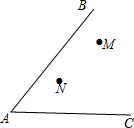 如图,南开中学高二年级的学生分别在五云山寨M,N两处参加社会时间活动.先要在道路AB,AC形成的锐角∠BAC内设一个休息区P,使P到两条道路的距离相等,并且使得PM=PN,请用直尺和圆规作出P点的位置(不写作法,值保留作图痕迹).
如图,南开中学高二年级的学生分别在五云山寨M,N两处参加社会时间活动.先要在道路AB,AC形成的锐角∠BAC内设一个休息区P,使P到两条道路的距离相等,并且使得PM=PN,请用直尺和圆规作出P点的位置(不写作法,值保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com