
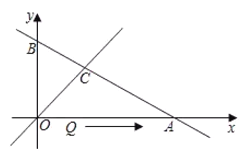
【题目】如图,直线![]() 与坐标轴分别交于点
与坐标轴分别交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的长为___________.
的长为___________.
【答案】2或![]() 或4
或4
【解析】
先求出直线![]() 与直线
与直线![]() 交点C的坐标,若使
交点C的坐标,若使![]() 是等腰三角形,分三种情况讨论,即OQ=CQ或OC=OQ或OC=CQ,在直角三角形中利用勾股定理,根据等腰三角形的性质即可求出OQ.
是等腰三角形,分三种情况讨论,即OQ=CQ或OC=OQ或OC=CQ,在直角三角形中利用勾股定理,根据等腰三角形的性质即可求出OQ.
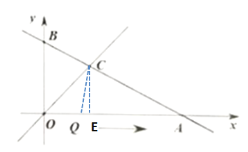
①如图,当OQ=CQ时,过点C作CE⊥OA于点E,
直线![]() 与直线
与直线![]() 交于点C,
交于点C,
![]()
得x=2,
y=x=2
∴C(2,2)
设OQ=CQ=x,QE=2-x
在Rt△CEQ中![]()
解得x=2
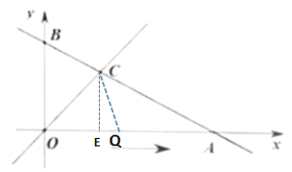
②当OC=OQ时,过点C作CE⊥OA于点E,C(2,2)
在Rt△CEO中, ![]()
OC=![]()
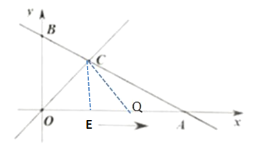
③当OC=CQ时, 过点C作CE⊥OA于点E
∵OC=CQ
∴OE=EQ=2
∴OQ=2OE=4
综上所示,若![]() 是等腰三角形,OQ的长为2或
是等腰三角形,OQ的长为2或![]() 或4
或4
故答案为:2或![]() 或4
或4


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)用等式表示线段BH与AE的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B(a,b)在第一象限,过B作BA⊥y轴于A,过B作BC⊥x轴于C,且实数a、b满足(a-b-2)2+|2a+b-10|≤0,含45角的Rt△DEF的一条直角边DF与x轴重合,DE⊥x轴于D,点F与坐标原点重合,DE=DF=3.△DEF从某时刻开始沿着坐标轴以1个单位长度每秒的速度匀速运动,运动时间为t秒.
(1)求点B的坐标;
(2)若△DEF沿着y轴负方向运动,连接AE,EG平分∠AEF,EH平分∠AED,当EG∥DF时,求∠HEF的度数;
(3)若△DEF沿着x轴正方向运动,在运动过程中,记△AEF与长方形OABC重叠部分的面积为S,当0<t≤4,S=![]() 时,请你求出运动时间t.
时,请你求出运动时间t.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,F、G是AD边上的两个点,且FC平分∠BCD,GB平分∠ABC,FC与GB交于点E.
①AB=AG;②连接BF、CG,则四边形BFGC为等腰梯形;③AF=DG;④△ABG∽△DCF.
以上四个结论中一定成立的有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com