【题目】如图的三角形纸片中，AB=AC，BC=12cm，∠C=30°，折叠这个三角形，使点B落在AC的中点D处，折痕为EF，那么BF的长为cm． 
【答案】
【解析】解：过D作DH⊥BC，过点A作AN⊥BC于点N，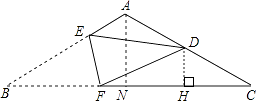 
∵AB=AC，
∴∠B=∠C=30°，
根据折叠可得：DF=BF，∠EDF=∠B=30°，
∵AB=AC，BC=12cm，
∴BN=NC=6cm，
∵点B落在AC的中点D处，AN∥DH，
∴NH=HC=3cm，
∴DH=3tan30°= 
（cm），
设BF=DF=xcm，则FH=12﹣x﹣3=9﹣x（cm），
故在Rt△DFC中，DF2=DH2+FH2 ，
故x2=（ ）2+（9﹣x）2 ，
解得：x= ，
即BF的长为： cm．
故答案为： ．
首先过D作DH⊥BC，过点A作AN⊥BC于点N，根据题意结合等腰三角形的性质进而得出CN的长，再利用锐角三角函数关系以及勾股定理得出答案．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
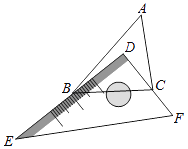
【题目】有一块直角三角板DEF放置在△ABC上，三角板DEF的两条直角边DE、DF恰好分别经过点B、C．△ABC中，∠A=50°，求∠DBA+∠DCA的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，EF//AD，
＝
.说明：∠DGA+∠BAC=180°. 填空并写出推理的依据．
解：∵EF//AD，（已知）
∴＝__ __ (_____________________________)
又∵＝， （已知）
∴＝__ _， （等量替代）
∴AB//___ ___， (_______________ _____________)
∴∠DGA+∠BAC=180° (_______________ _________)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了了解某校学生进行课外阅读的情况，从全校2200名学生中随机抽取了100名学生，对他们平均每天进行课外阅读的时长进行统计，样本容量是_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校八年级学生在学习《数据的分析》后，进行了检测，现将该校八（1）班学生的成绩统计如下表，并绘制成条形统计图（不完整）． 
分数（分） | 人数（人） |
68 | 4 |
78 | 7 |
80 | 3 |
88 | 5 |
90 | 10 |
96 | 6 |
100 | 5 |
（1）补全条形统计图；
（2）该班学生成绩的平均数为86.85分，写出该班学生成绩的中位数和众数；
（3）该校八年级共有学生500名，估计有多少学生的成绩在96分以上（含96分）？
（4）小明的成绩为88分，他的成绩如何，为什么？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简，再求值：
(1)(1＋a)(1－a)＋(a－2)2，其中a＝
；
(2)(2x＋3)(2x－3)－4x(x－1)＋(x－2)2，其中x＝－3.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线l3上有点P（点P与点C、D不重合），点A在直线l1上，点B在直线l2上。
（1）如果点P在C、D之间运动时，试说明∠1+∠3=∠2；
（2）如果点P在直线l1的上方运动时，试探索∠1，∠2，∠3之间的关系又是如何？
（3）如果点P在直线l2的下方运动时，试探索∠PAC，∠PBD，∠APB之间的关系又是如何？ （直接写出结论）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB＝10，AC＝2
，BC边上的高AD＝6，则另一边BC等于_______．
【答案】10或6
【解析】试题解析：根据题意画出图形，如图所示，
如图1所示，AB=10，AC=2，AD=6，
在Rt△ABD和Rt△ACD中，
根据勾股定理得：BD=
=8，CD=
=2，
此时BC=BD+CD=8+2=10；
如图2所示，AB=10，AC=2，AD=6，
在Rt△ABD和Rt△ACD中，
根据勾股定理得：BD==8，CD==2，
此时BC=BD-CD=8-2=6，
则BC的长为6或10．
【题型】填空题
【结束】
12
【题目】在平面直角坐标系中，已知一次函数y=2x+1的图象经过P1（x1，y1）、P2（x2，y2）两点，若x1＜x2，则y1 ______ y2．（填“＞”“＜”或“=”）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com