
分析 (1)根据题意归纳总结得到一般性规律,写出即可;
(2)利用作差法比较即可.
解答 解:(1)根据题意得:$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\sqrt{n+1}$-$\sqrt{n}$;
(2)∵($\sqrt{11}$-$\sqrt{10}$)-($\sqrt{12}$-$\sqrt{10}$)=$\sqrt{11}$-$\sqrt{10}$-$\sqrt{12}$+$\sqrt{10}$=$\sqrt{11}$-$\sqrt{12}$<0,
∴$\sqrt{11}$-$\sqrt{10}$<$\sqrt{12}$-$\sqrt{10}$,
故答案为:<
点评 此题考查了分母有理化,正确选择两个二次根式,使它们的积符合平方差公式是解答问题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
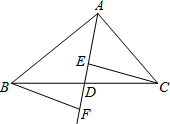 如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件DE=DF,使得△BDF≌△CDE,依据是SAS.
如图,在△ABC中,点D是BC的中点,作射线AD,在线段AD及其延长线上分别取点E、F,连接CE、BF.添加一个条件DE=DF,使得△BDF≌△CDE,依据是SAS.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com