
【题目】阅读下列材料: 如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)根据以上材料解决下列问题: 如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= ![]() .
.
①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
【答案】
(1)(x﹣3)2+y2=1;(x+1)2+(y+2)2=3
(2)①证明:∵BD⊥OC,
∴CD=OD,
∴BE垂直平分OC,
∴EO=EC,
∴∠EOC=∠ECO,
∵BO=BC,
∴∠BOC=∠BCO,
∴∠EOC+∠BOC=∠ECO+∠BCO,
∴∠BOE=∠BCE=90°,
∴BC⊥CE,
∴EC是⊙B的切线;
②存在.
∵∠BOE=∠BCE=90°,
∴点C和点O偶在以BE为直径的圆上,
∴当P点为BE的中点时,满足PB=PC=PE=PO,
∵B点坐标为(﹣6,0),
∴OB=6,
∵∠AOC+∠DOE=90°,∠DOE+∠BEO=90°,
∴∠BEO=∠AOC,
∴sin∠BEO=sin∠AOC= ![]() ,
,
在Rt△BOE中,sin∠BEO= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BE=10,
∴OE= ![]() =8,
=8,
∴E点坐标为(0,8),
∴线段AB的中点P的坐标为(﹣3,4),PB=5,
∴以P(﹣3,4)为圆心,以5为半径的⊙P的方程为(x+3)2+(y﹣4)2=25.
【解析】(1)解:①以A(3,0)为圆心,1为半径的圆的方程为(x﹣3)2+y2=1; ②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为(x+1)2+(y+2)2=3;
为半径的圆的方程为(x+1)2+(y+2)2=3;
所以答案是(x﹣3)2+y2=1;(x+1)2+(y+2)2=3;
【考点精析】关于本题考查的等腰三角形的性质和勾股定理的概念,需要了解等腰三角形的两个底角相等(简称:等边对等角);直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能得出正确答案.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
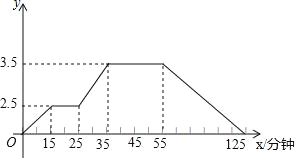
【题目】如图所示的图象反映的过程是:小强星期天从家跑步去体育场,在那里锻炼了一会儿后又走到文具店去买笔,然后步行回家,其中x表示时间,y表示小强离家的距离,根据图象回答下列问题.
(1)体育场离小强家有多远?小强从家到体育场用了多长时间?
(2)体育场距文具店多远?
(3)小强在文具店逗留了多长时间?
(4)小强从文具店回家的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
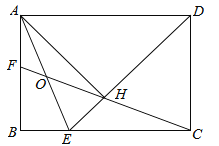
【题目】(3分)如图,在矩形ABCD中,BC=![]() AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
①∠AEB=∠AEH;②DH=![]() EH;③HO=
EH;③HO=![]() AE;④BC﹣BF=
AE;④BC﹣BF=![]() EH.
EH.
其中正确命题的序号是 (填上所有正确命题的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
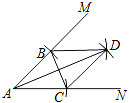
【题目】如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于![]() BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.若∠MBD=40°,则∠NCD的度数为_____.
BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.若∠MBD=40°,则∠NCD的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛交运集团出租车司机张师傅某天下午的营运全是在东西走向的吉林路上进行的,如果规定向东为正,向西为负,他这天下午行车里程![]() 单位:千米
单位:千米![]() 如下:
如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)张师傅这天最后到达目的地时,在下午出车时的出发地哪个方向?距离出发地多远?
(2)张师傅这天下午共行车多少千米?
(3)若每千米耗油![]() ,则这天下午张师傅用了多少升油?
,则这天下午张师傅用了多少升油?
查看答案和解析>>
科目:初中数学 来源: 题型:
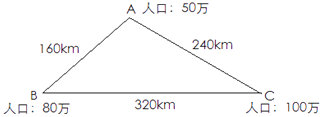
【题目】据有关资料统计,两个城市之间每天的电话通话次数T与这两个城市的人口数xy(单位:万人)以及两城市间的距离l(单位:km)之间有下列关系式![]() (k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
(k为常数) 己知A,B,C三个城市的人口数及它们之间的距离如图所示如果A,B两个城市间每天的电话通话次数为n,求B,C两个城市间每天的电话通话次数(用含n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
①最大的负整数是﹣1;②数轴上表示数2 和﹣2的点到原点的距离相等;③当a≤0时,|a|=﹣a成立;④a的倒数是![]() ;⑤(﹣2)2 和﹣22相等.
;⑤(﹣2)2 和﹣22相等.
A. 2 个 B. 3 个 C. 4 个 D. 5 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】猜想与证明: 如图,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM,EM.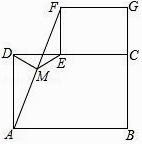
(1)试猜想写出DM与EM的数量关系,并证明你的结论. 拓展与延伸:
(2)若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则(1)中的结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的有( )
①一个三角形至少有2个锐角;②在△ABC中,若∠A=2∠B=3∠C,则△ABC为直角三角形;③过n边形的一个顶点可作(n﹣3)条对角线;④n边形每增加一条边,则其内角和增加360°.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com