
| A. | -2017 | B. | c | C. | 0 | D. | c-2017 |
分析 根据函数y=x2+bx+c的图象与x轴只有一个交点得出顶点坐标为(-$\frac{b}{2}$,0),对称轴为x=-$\frac{b}{2}$,由二次函数图象的对称性得出$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{b}{2}$,即可得出答案.
解答 解:∵函数y=x2+bx+c的图象与x轴只有一个交点,
∴顶点坐标为(-$\frac{b}{2}$,0),对称轴为x=-$\frac{b}{2}$,
∵(x1,2017)、(x2,2017)是该函数图象上的两个点,
∴$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{b}{2}$,
∴当x=$\frac{{x}_{1}+{x}_{2}}{2}$时,函数值y=0;
故选:C.
点评 本题主要考查了抛物线与x轴交点、二次函数图象上点的坐标特征;根据函数y=x2+bx+c的图象与x轴只有一个交点得出顶点坐标为(-$\frac{b}{2}$,0)是解决问题的关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
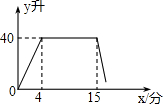 妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:
妈妈在用洗衣机洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示,根据图象解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
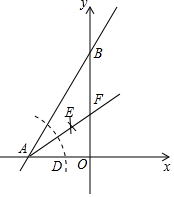 如图,在平面直角坐标系中,一次函数y=$\sqrt{3}$x+1的图象分别与x轴、y轴交于A、B两点,以A为圆心,适当长为半径画弧分别交AB、AO于点C、D,再分别以C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧交于点E,连接AE并延长交y轴于点F,则下列说法正确的个数是( )
如图,在平面直角坐标系中,一次函数y=$\sqrt{3}$x+1的图象分别与x轴、y轴交于A、B两点,以A为圆心,适当长为半径画弧分别交AB、AO于点C、D,再分别以C、D为圆心,大于$\frac{1}{2}$CD的长为半径画弧,两弧交于点E,连接AE并延长交y轴于点F,则下列说法正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
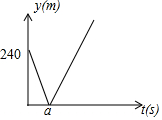 甲,乙两人沿同一条滨海大道同起点、同方向进行体育锻炼,已知甲匀速跑步,先出发60s,乙匀速骑车,速度是甲的两倍,在锻炼的过程中,设甲乙两人相距y(m),乙骑车的时间为t(s),y是t的函数,其图象的一部分如图所示.
甲,乙两人沿同一条滨海大道同起点、同方向进行体育锻炼,已知甲匀速跑步,先出发60s,乙匀速骑车,速度是甲的两倍,在锻炼的过程中,设甲乙两人相距y(m),乙骑车的时间为t(s),y是t的函数,其图象的一部分如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-$\frac{1}{2}$x-6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.
如图,抛物线y=-x2+bx+c与直线AB交于A(-4,-4),B(0,4)两点,直线AC:y=-$\frac{1}{2}$x-6交y轴于点C.点E是直线AB上的动点,过点E作EF⊥x轴交AC于点F,交抛物线于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com