
【题目】如图,![]() 中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①
中,AB=AC,D、E分别在边AB、AC上,且满足AD=AE.下列结论中:①![]() ;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若
;②AO平分∠BAC;③OB=OC;④AO⊥BC;⑤若![]() ,则
,则![]() ;其中正确的有( )
;其中正确的有( )

A. 2个B. 3个C. 4个D. 5个
【答案】D
【解析】
利用SAS可证明△ABE≌△ACD,判断①正确;根据全等三角形的性质以及邻补角定义可得∠BDO=∠BEC,继而利用AAS证明△BOD≌△COE,可得OD=OE,BO=OC,判断③正确;利用SSS证明△AOD≌△AOE,可得AO平分∠BAC,判断②正确,继而根据等腰三角形三线合一的性质可判断④正确,根据三角形的高相等时,两三角形的面积比就是底边之比,通过推导可判断⑤正确.
在△ABE与△ACD中,
 ,
,
∴△ABE≌△ACD,故①正确;
∴∠AEB=∠ADC,
∴∠BDO=∠BEC,
∵AB=AC,AD=AE,∴BD=CE,
在△BOD与△COE中,
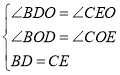 ,
,
∴△BOD≌△COE,
∴OD=OE,BO=OC,故③正确;
在△AOD与△AOE中,
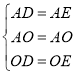 ,
,
∴△AOD≌△AOE,
∴∠DAO=∠EAO,
即AO平分∠BAC,故②正确,
又∵AB=AC,
∴AO⊥BC,故④正确,
∵![]() ,
,
∴S△BOD=2S△AOD,
又∵△BOD≌△COE,
∴S△COE=2S△AOD,
又∵△AOD≌△AOE,
∴S△AOC=3S△AOD,
∴OC=3OD,
即![]() ,故⑤正确,
,故⑤正确,
故选D.


科目:初中数学 来源: 题型:
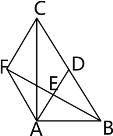
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1) 求证:AF=DC;
(2) 若AC⊥AB,试判断四边形ADCF的形状,并说明理由;
(3) 当△ABC满足什么条件时,四边形ADCF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
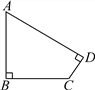
【题目】如图所示,在四边形ABCD中,∠B=∠D=90°,AB=BC=15千米,CD=3![]() 千米.求四边形ABCD的周长和面积(结果保留整数,参考数据:
千米.求四边形ABCD的周长和面积(结果保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45).
≈2.45).
查看答案和解析>>
科目:初中数学 来源: 题型:
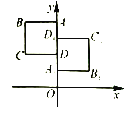
【题目】如图,正方形ABCD 与正方形![]() 关于某点中心对称.已知A,
关于某点中心对称.已知A,![]() ,D三点的坐标分别是(0,4),(0,3),(0,2).
,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)求对称中心的坐标:
(2)写出顶点B,C,![]() 的坐标。
的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
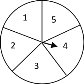
【题目】如图,转盘中5个扇形的面积都相等,任意转动转盘一次,当转盘停止转动时,把下列事件:①指针落在标有3的区域内;②指针落在标有奇数的区域;③指针落在标有6的区域内;④指针落在标有偶数或奇数的区域,的序号按发生的可能性从小到大的顺序排列为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学团委组织学生去儿童福利院慰问,准备购买15个甲种文具和20个乙种文具,共需885元;后翻阅商场海报发现,下周甲、乙两种文具进行促销活动,甲种文具打八折销售、乙种文具打九折,且打折后两种文具的销售单价相同.
(1)求甲、乙两种文具的原销售单价各为多少元?
(2)购买打折后的15个甲种文具和20个乙种文具,共可节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
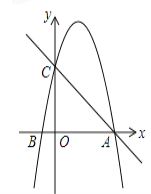
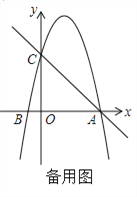
【题目】如图,在平面直角坐标系中,已知点A 的坐标是(4,0),并且0A=OC=4OB,动点P在过A,B,C三点的抛物线上.
(1) 求抛物线的解析式;
(2)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线,垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标;
(3) 是否存在点P,使得△ACP是以AC为直角边的直角三角形? 若存在,求出所有符合条件的点P的坐标; 若不存在,说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com