
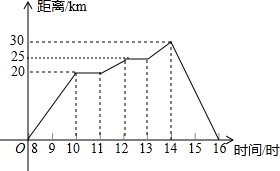
 假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.
假日里,小亮和爸爸骑自行车郊游,上午8时从家出发,16时返回家中,他们离家的距离与时间的关系可用图中的折线表示.分析 (1)从图象上可以知道,小亮到达离家最远的地方是在14时,最远距离是30千米;
(2)在图象开始处于水平状态的时刻就是小亮第一次休息的时刻;
(3)在这段时刻,我们看纵坐标时,两点对应的路程差即是小亮骑车的路程;
(4)由图形可知,回去时小亮是匀速行驶,中间没有休息,故速度是路程除以所用的时间.
解答 解:(1)由图象知,在图形的最高点就是小亮到达离家最远30千米的地方.此时对应的时刻是14时.
(2)休息的时候路程为0,即开始出现的第一个水平状态的时刻,由图象可知,小亮第一次休息的时刻是在10时.
(3)由图象知,在这段时间内,小亮只在11时到12时运动,对应的路程差为5km.
(4)返回时,小亮为匀速运动,路程为30千米,所用时间是2小时,故速度为15千米/小时.
点评 此题考查函数的图象问题,关键是考查学生的识图能力,要求学生学会使用数形结合的思想.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,一架云梯AB斜靠在一面墙上,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿底面向右滑行.
如图所示,一架云梯AB斜靠在一面墙上,设木棍的中点为P.若木棍A端沿墙下滑,且B端沿底面向右滑行.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
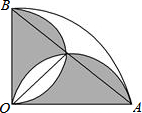 半径1cm,圆心角90度的扇形OAB中,分别以OA,OB为直径作半圆,则阴影部分(两个半圆除了重叠部分其余部分)面积为$\frac{1}{2}$.
半径1cm,圆心角90度的扇形OAB中,分别以OA,OB为直径作半圆,则阴影部分(两个半圆除了重叠部分其余部分)面积为$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
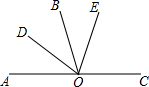 已知,O是直线AC上一点,OD平分∠AOB,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=72°,OB是∠DOE的平分线吗?说明理由.
已知,O是直线AC上一点,OD平分∠AOB,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=72°,OB是∠DOE的平分线吗?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知在等腰三角形ABC中,D是BC边上一点,DE⊥AB,DF⊥AC,E,F分别为垂足,若DF+DE=2$\sqrt{2}$,△ABC的面积为$\sqrt{24}$+$\sqrt{8}$,求AB的长.
已知在等腰三角形ABC中,D是BC边上一点,DE⊥AB,DF⊥AC,E,F分别为垂足,若DF+DE=2$\sqrt{2}$,△ABC的面积为$\sqrt{24}$+$\sqrt{8}$,求AB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com