
【题目】如图是轮滑场地的截面示意图,平台AB距x轴(水平)18米,与y轴交于点B,与滑道y=![]() (x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(x≥1)交于点A,且AB=1米.运动员(看成点)在BA方向获得速度v米/秒后,从A处向右下飞向滑道,点M是下落路线的某位置.忽略空气阻力,实验表明:M,A的竖直距离h(米)与飞出时间t(秒)的平方成正比,且t=1时h=5,M,A的水平距离是vt米.
(1)求k,并用t表示h;
(2)设v=5.用t表示点M的横坐标x和纵坐标y,并求y与x的关系式(不写x的取值范围),及y=13时运动员与正下方滑道的竖直距离;
(3)若运动员甲、乙同时从A处飞出,速度分别是5米/秒、v乙米/秒.当甲距x轴1.8米,且乙位于甲右侧超过4.5米的位置时,直接写出t的值及v乙的范围.
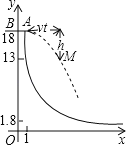
【答案】(1)k=18,h=5t2;(2)x=5t+1,y=﹣5t2+18,y=![]() ,当y=13时,运动员在与正下方滑道的竖直距离是10米;(3)t=1.8,v乙>7.5
,当y=13时,运动员在与正下方滑道的竖直距离是10米;(3)t=1.8,v乙>7.5
【解析】(1)用待定系数法解题即可;
(2)根据题意,分别用t表示x、y,再用代入消元法得出y与x之间的关系式;
(3)求出甲距x轴1.8米时的横坐标,根据题意求出乙位于甲右侧超过4.5米的v乙.
(1)由题意,点A(1,18)代入y=![]() ,
,
得:18=![]() ,
,
∴k=18,
设h=at2,把t=1,h=5代入,
∴a=5,
∴h=5t2;
(2)∵v=5,AB=1,
∴x=5t+1,
∵h=5t2,OB=18,
∴y=﹣5t2+18,
由x=5t+1,
则t=![]() (x-1),
(x-1),
∴y=﹣![]() (x-1)2+18=
(x-1)2+18=![]() ,
,
当y=13时,13=﹣![]() (x-1)2+18,
(x-1)2+18,
解得x=6或﹣4,
∵x≥1,
∴x=6,
把x=6代入y=![]() ,
,
y=3,
∴运动员在与正下方滑道的竖直距离是13﹣3=10(米);
(3)把y=1.8代入y=﹣5t2+18
得t2=![]() ,
,
解得t=1.8或﹣1.8(负值舍去)
∴x=10
∴甲坐标为(10,1.8)恰号落在滑道y=![]() 上,
上,
此时,乙的坐标为(1+1.8v乙,1.8),
由题意:1+1.8v乙﹣(1+5×1.8)>4.5,
∴v乙>7.5.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H .下列结论:
①∠DBE=∠F;②∠F=∠BAC-∠C;
③2∠BEF=∠BAF+∠C;④∠BGH=∠ABE+∠C.其中正确的有( )
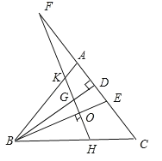
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 且
且![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 在数轴上对应的数.
在数轴上对应的数.
(1)求点![]() 与点
与点![]() 的距离;
的距离;
(2)若甲、乙两个动点分别从![]() 、
、![]() 两点同时出发,沿数轴正方向运动,它们的速度分别是2和1(单位长度/秒),求甲追上乙时所用的时间;
两点同时出发,沿数轴正方向运动,它们的速度分别是2和1(单位长度/秒),求甲追上乙时所用的时间;
(3)在(2)的条件下,甲动点向数轴正方向运动,乙动点向数轴负方向运动.当甲动点开始运动时,丙动点以4个单位长度/秒的速度和甲动点同时从点![]() 向数轴正方向运动,当丙动点遇到乙动点时立即返回向数轴负方向运动,当遇到甲动点时也马上返回,如此往复直到甲乙两动点相遇则停止运动,设甲乙两动点在点
向数轴正方向运动,当丙动点遇到乙动点时立即返回向数轴负方向运动,当遇到甲动点时也马上返回,如此往复直到甲乙两动点相遇则停止运动,设甲乙两动点在点![]() 处相遇,求从开始到停止运动,丙动点走的总路程以及点
处相遇,求从开始到停止运动,丙动点走的总路程以及点![]() 对应的数字.
对应的数字.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在数轴上对应的数为26,以原点O为圆心,OA为半径作优弧![]() ,使点B在O右下方,且tan∠AOB=
,使点B在O右下方,且tan∠AOB=![]() ,在优弧
,在优弧![]() 上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
上任取一点P,且能过P作直线l∥OB交数轴于点Q,设Q在数轴上对应的数为x,连接OP.
(1)若优弧上一段![]() 的长为13π,求∠AOP的度数及x的值;
的长为13π,求∠AOP的度数及x的值;
(2)求x的最小值,并指出此时直线l与![]() 所在圆的位置关系;
所在圆的位置关系;
(3)若线段PQ的长为12.5,直接写出这时x的值.
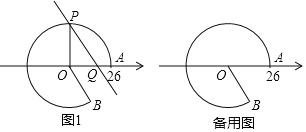
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,AB=AC=12cm,BC=9cm,若点Q在线段CA上以4cm/s的速度由点C向点A运动,点P在BC线段上以3cm/s的速度由B向C运动,求多长时间点Q与点P第一次在哪条边上相遇?( )
A.24s BC边B.12s BC边
C.24s AB边D.12s AC边
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业1~5月份利润的变化情况图所示,以下说法与图中反映的信息相符的是( )
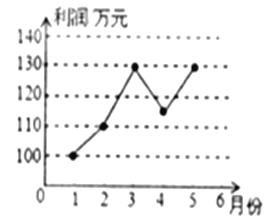
A. 1~3月份利润的平均数是120万元
B. 1~5月份利润的众数是130万元
C. 1~5月份利润的中位数为120万元
D. 1~2月份利润的增长快于2~3月份利润的增长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com