
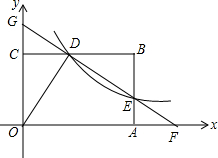
 如图,反比例函数y=$\frac{4}{x}$(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交与点E,直线DE与x轴、y轴分别交于点F、G.若△ODG与△ODF的面积比为2:7,则矩形ABCO的面积是14.
如图,反比例函数y=$\frac{4}{x}$(x>0)的图象与矩形ABCO的边BC交于点D,与边AB交与点E,直线DE与x轴、y轴分别交于点F、G.若△ODG与△ODF的面积比为2:7,则矩形ABCO的面积是14. 分析 设D(m,$\frac{4}{m}$),E(n,$\frac{4}{n}$),得到OC=AB=$\frac{4}{m}$,CD=m,AE=$\frac{4}{n}$,OA=BC=n,于是得到S矩形ABCO=AB•BC=$\frac{4n}{m}$,根据相似三角形的性质得到$\frac{CD}{BD}=\frac{DG}{DE}$,得到$\frac{m}{n-m}=\frac{DG}{DE}$,同理得到$\frac{m}{n-m}=\frac{EF}{DE}$,得到DG=EF,根据全等三角形的性质得到CD=AF=m,CG=AE=$\frac{4}{n}$,根据△ODG与△ODF的面积比为2:7,列方程得到$\frac{4n}{m}$=14,即可得到结论.
解答 解:设D(m,$\frac{4}{m}$),E(n,$\frac{4}{n}$),
∴OC=AB=$\frac{4}{m}$,CD=m,AE=$\frac{4}{n}$,OA=BC=n,
∴S矩形ABCO=AB•BC=$\frac{4n}{m}$,
∵∠GCD=∠B=90°,∠GDC=∠BDE,
∴△CDG∽△BDE,
∴$\frac{CD}{BD}=\frac{DG}{DE}$,
即$\frac{m}{n-m}=\frac{DG}{DE}$,
同理$\frac{AE}{BE}=\frac{EF}{DE}$,
即$\frac{\frac{4}{n}}{\frac{4}{m}-\frac{4}{n}}$=$\frac{EF}{DE}$,
∴$\frac{m}{n-m}=\frac{EF}{DE}$,
∴$\frac{DG}{DE}=\frac{EF}{DE}$,
∴DG=EF,
在△CDG与△AEF中,
$\left\{\begin{array}{l}{∠CDF=∠AFE}\\{∠DCG=∠FAE}\\{DG=EF}\end{array}\right.$,
∴△CDG≌△AEF,
∴CD=AF=m,CG=AE=$\frac{4}{n}$,
∵△ODG与△ODF的面积比为2:7,
∴$\frac{\frac{1}{2}OG•CD}{\frac{1}{2}OF•OC}$=$\frac{2}{7}$,
∴$\frac{(\frac{4}{m}+\frac{4}{n})m}{(m+n)•\frac{4}{m}}=\frac{2}{7}$,
∴$\frac{4n}{m}$=14(负值舍去),
∴矩形ABCO的面积是14.
故答案为:14.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|,主要通过设点的坐标结合矩形性质、反比例函数解析式及三角形全等表示出所需线段的长是关键.


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
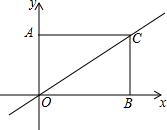 有一矩形AOBC放在如图所示的直角坐标系,一正比例函数的图象经过点C,且矩形的两边满足2OA=AC.
有一矩形AOBC放在如图所示的直角坐标系,一正比例函数的图象经过点C,且矩形的两边满足2OA=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
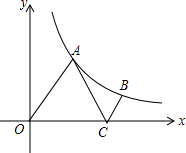 如图,点A,B在反比例函数y=$\frac{m}{x}$的图象上,点A的坐标为($\sqrt{3}$,3),点C在x轴上,且使△AOC是等边三角形,BC∥OA.
如图,点A,B在反比例函数y=$\frac{m}{x}$的图象上,点A的坐标为($\sqrt{3}$,3),点C在x轴上,且使△AOC是等边三角形,BC∥OA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
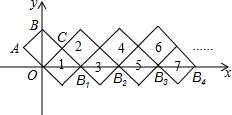 如图,在平面直角坐标系中放置一正方形OABC,OA=1,点B在y轴上,正方形1,2,3…是由正方形OABC通过某种变化得到的,正方形的顶点B1,B2,B3,…都在x轴上,按此规律,第n个正方形右侧顶点的横坐标是$\frac{n+1}{2}$$\sqrt{2}$.
如图,在平面直角坐标系中放置一正方形OABC,OA=1,点B在y轴上,正方形1,2,3…是由正方形OABC通过某种变化得到的,正方形的顶点B1,B2,B3,…都在x轴上,按此规律,第n个正方形右侧顶点的横坐标是$\frac{n+1}{2}$$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
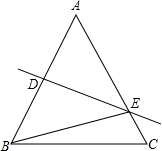 如图,在等腰△ABC中,AB=AC=20,DE垂直平分AB.
如图,在等腰△ABC中,AB=AC=20,DE垂直平分AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -5(a-b)2 | B. | 5(b-a)2 | C. | -(a-b)2 | D. | (b-a)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com