
【题目】解不等式组: ![]() .请结合题意填空,完成本体的解法.
.请结合题意填空,完成本体的解法. ![]()
(1)解不等式(1),得;
(2)解不等式(2),得;
(3)把不等式 (1)和 (2)的解集在数轴上表示出来.
(4)原不等式的解集为 .
【答案】
(1)x<5
(2)x≥2
(3)解:把不等式 (1)和 (2)的解集在数轴上表示为:
![]()
(4)2≤x<5
【解析】解:(1)去括号得,5>3x﹣12+2, 移项得,5+12﹣2>3x,
合并同类项得,15>3x,
把x的系数化为1得,x<5.
所以答案是:x<5;
·(2)移项得,2x≥1+3,
合并同类项得,2x≥4,
x的系数化为1得,x≥2.
所以答案是:x≥2;
·(4)由(3)得,原不等式的解集为:2≤x<5.
所以答案是:2≤x<5.
【考点精析】掌握不等式的解集在数轴上的表示和一元一次不等式组的解法是解答本题的根本,需要知道不等式的解集可以在数轴上表示,分三步进行:①画数轴②定界点③定方向.规律:用数轴表示不等式的解集,应记住下面的规律:大于向右画,小于向左画,等于用实心圆点,不等于用空心圆圈;解法:①分别求出这个不等式组中各个不等式的解集;②利用数轴表示出各个不等式的解集;③找出公共部分;④用不等式表示出这个不等式组的解集.如果这些不等式的解集的没有公共部分,则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 ).


科目:初中数学 来源: 题型:
【题目】在社会主义新农村建设中,衢州某乡镇决定对A、B两村之间的公路进行改造,并有甲工程队从A村向B村方向修筑,乙工程队从B村向A村方向修筑.已知甲工程队先施工3天,乙工程队再开始施工.乙工程队施工几天后因另有任务提前离开,余下的任务有甲工程队单独完成,直到公路修通.下图是甲乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数图象,请根据图象所提供的信息解答下列问题:

(1)乙工程队每天修公路多少米?
(2)分别求甲、乙工程队修公路的长度y(米)与施工时间x(天)之间的函数关系式.
(3)若该项工程由甲、乙两工程队一直合作施工,需几天完成?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=6,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是( ) 
A.6
B.6.25
C.6.5
D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月28日-12月31日,山东临沂灯展中千万盏彩灯点亮300亩天然花海.某日,从晚上17时开始每小时进入灯展的人数约为900人(之前该灯展有游客400人),同时每小时走出灯展的人数约为600人,已知该灯展的饱和人数约为1600人,则该灯展人数饱和时的时间约为( )
A. 21时 B. 22时 C. 23时 D. 24时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板叠在一起如图放置,最小锐角的顶点D恰好放在等腰直角三角板的斜边AB上,BC与DE交于点M.如果∠ADF=100°,那么∠BMD为度. 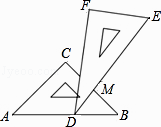
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 的图像经过点
的图像经过点![]() .
.
(1)求k的值,并判断点![]() 是否在该反比例函数的图像上;
是否在该反比例函数的图像上;
(2)该反比例函数图像在第______象限,在每个象限内,y随x的增大而_______.
(3)当![]() 时,求y的取值范围.
时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD置于直角坐标系中,AB∥x轴,BC∥y轴,AB=4,BC=3,点B(5,1)翻折矩形纸片使点A落在对角线DB上的H处得折痕DG.
(1)求AG的长;
(2)在坐标平面内存在点M(m,﹣1)使AM+CM最小,求出这个最小值;
(3)求线段GH所在直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+2xa+c经过A(﹣4,0),B(0,4)两点,与x轴交于另一点C,直线y=x+5与x轴交于点D,与y轴交于点E.
(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,连接EP,过点E作EP的垂线l,在l上截取线段EF,使EF=EP,且点F在第一象限,过点F作FM⊥x轴于点M,设点P的横坐标为t,线段FM的长度为d,求d与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,过点E作EH⊥ED交MF的延长线于点H,连接DH,点G为DH的中点,当直线PG经过AC的中点Q时,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com