
| 月用水量(m3) | 4 | 6 | 7 | 12 | 14 | 15 |
| 户数 | 2 | 4 | 6 | 2 | 2 | 4 |
分析 (1)根据样本和样本容量的定义回答即可;
(2)用加权平均数的计算公式计算即可.
(3)用样本平均数估计总体平均数.
解答 解:(1)样本是其中20户家庭自来水用水量;样本容量是20;
故答案为:其中20户家庭自来水用水量,20.
(2)平均用水量为:$\frac{1}{20}$(4×2+6×4+7×6+12×2+14×2+15×4)
=$\frac{1}{20}$(8+24+42+24+28+60)=$\frac{186}{20}$=9.3m3;
(3)估计该小区300户家庭的月总用水量为:300×9.3=2790m3.
点评 考查了用样本估计总体,加权平均数的定义等知识,生活中常遇到的估算问题,通常采用样本估计总体的方法.


科目:初中数学 来源: 题型:解答题
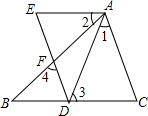 完成证明,说明理由.
完成证明,说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
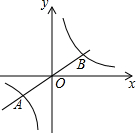 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$相交于A(-2,n)、B两点,则k的值为( )
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$相交于A(-2,n)、B两点,则k的值为( )| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
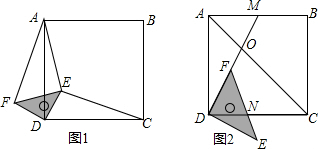
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
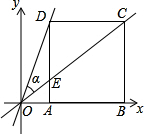 边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.
边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com