
【题目】如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④PC平分∠APB;⑤∠APD=60°,其中正确结论有( )
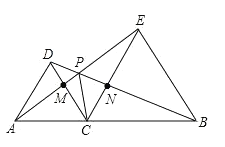
A.①②③④⑤B.①②④⑤C.①②③⑤D.①②⑤
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
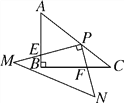
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4.Rt△MPN中,∠MPN=90°,点P在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:![]() ≈1.73,
≈1.73,![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
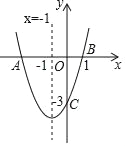
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
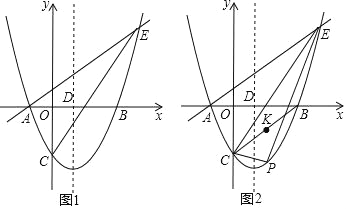
【题目】如图,在平面直角坐标系中,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴x轴交于点D,点E(4,n)在抛物线上.
(1)求直线AE的解析式;
(2)连接CB,点K是线段CB的中点,点M是y轴上的一点,点P为直线CE下方抛物线上的一点,连接PC,PE,当△PCE的面积最大时,求KM+PM的最小值;
(3)点G是线段CE的中点,将抛物线y=x2﹣2x﹣3沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F,在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国是世界上13个贫水国家之一.某校有800名在校学生,学校为鼓励学生节约用水,展开“珍惜水资源,节约每一滴水”系列教育活动.为响应学校号召,数学小组做了如下调查:
小亮为了解一个拧不紧的水龙头的滴水情况,记录了滴水时间和烧杯中的水面高度,如图1.小明设计了调查问卷,在学校随机抽取一部分学生进行了问卷调查,并制作出统计图.如图2和图3.
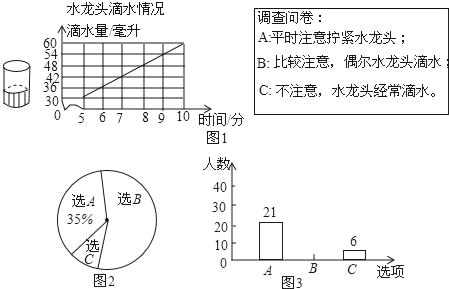
经结合图2和图3回答下列问题:
(1)参加问卷调查的学生人数为 人,其中选C的人数占调查人数的百分比为 .
(2)在这所学校中选“比较注意,偶尔水龙头滴水”的大概有 人.若在该校随机抽取一名学生,这名学生选B的概率为 .
请结合图1解答下列问题:
(3)在“水龙头滴水情况”图中,水龙头滴水量(毫升)与时间(分)可以用我们学过的哪种函数表示?请求出函数关系式.
(4)为了维持生命,每人每天需要约2400毫升水,该校选C的学生因没有拧紧水龙头,2小时浪费的水可维持多少人一天的生命需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:

其中有三天的个数墨汁覆盖了,但小强己经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是( )
A.![]() B.
B.![]() C.1D.
C.1D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 的顶点
的顶点![]() 与原点
与原点![]() 重合,点
重合,点![]() 在
在![]() 轴的
轴的
正半轴上,点![]() 在反比例函数
在反比例函数![]() 的图象上,点
的图象上,点![]() 的坐标为
的坐标为![]() .
.

![]() 求
求![]() 的值.
的值.
![]() 若将菱形
若将菱形![]() 向右平移,使点
向右平移,使点![]() 落在反比例函数
落在反比例函数![]() 的图象上,求菱形
的图象上,求菱形![]() 平移的距离.
平移的距离.
![]() 怎样平移可以使点
怎样平移可以使点![]() 、
、![]() 同时落在第一象限的曲线上?
同时落在第一象限的曲线上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com