
已知抛物线抛物线y n=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为( , );
依此类推第n条抛物线yn的顶点坐标为( , );
所有抛物线的顶点坐标满足的函数关系是 ;
(3)探究下列结论:
①若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
②是否存在经过点A(2,0)的直线和所有抛物线都相交,且被每一条抛物线截得得线段的长度都相等?若存在,直接写出直线的表达式;若不存在,请说明理由.
【答案】解:(1)∵y1=—(x—a1)2+a1与x轴交于点A0(0,0),
 ∴—a12+ a1=0,∴a1=0或1.
∴—a12+ a1=0,∴a1=0或1.
由已知可知a1>0,
∴a1=1.
即y1=—(x—1)2+1
方法一:令y1=0代入得:—(x—1)2+1=0,
∴x1=0,x2=2,
∴y1与x轴交于A0(0,0),A1(2,0)
∴b1=2,
方法二:∵y1=—(x—a1)2+a1与x轴交于点A0(0,0),
∴—(b1—1)2+1=0,b1=2或0,b1=0(舍去).
∴b1=2.
又∵抛物线y2=—(x—a2)2+a2与x轴交于点A1(2,0),
∴—(2—a2)2+ a2=0,
∴a2=1或4,∵a2> a1,∴a2=1(舍去).
∴取a2=4,抛物线y2=—(x—4)2+4.
(2)(9,9);
(n2,n2)
y=x.
详解如下:
∵抛物线y2=—(x—4)2+4令y2=0代入得:—(x—4)2+4=0,
∴x1=2,x2=6.
∴y2与x轴交于点A1(2,0),A2(6,0).
又∵抛物线y3=—(x—a3)2+a3与x轴交于A2(6,0),
∴—(6—a3)2+a3=0
∴a3=4或9,∵a3> a3,∴a3=4(舍去),
即a3=9,∴抛物线y3的顶点坐标为(9,9).
由抛物线y1的顶点坐标为(1,1),y2的顶点坐标为(4,4),y3的顶点坐标为(9,9),依次类推抛物线yn的顶点坐标为(n2,n2).
∵所有抛物线的顶点的横坐标等于纵坐标,
∴顶点坐标满足的函数关系式是:y= x;
③∵A0(0,0),A1(2,0),
∴A0 A1=2.
又∵yn=—(x—n2)2+n2,
令yn=0,
∴—(x—n2)2+n2=0,
即x1=n2+n,x2=n2-n,
∴A n-1(n2-n,0),A n(n2+n,0),即A n-1 A n=( n2+n)-( n2-n)=2 n.
②存在.是平行于直线y=x且过A1(2,0)的直线,其表达式为y=x-2.
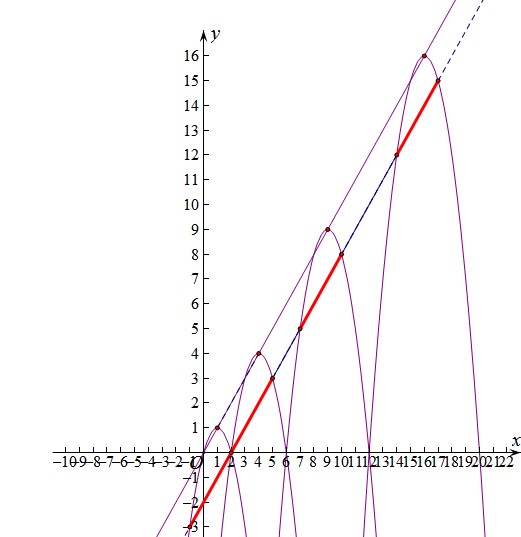
【考点解剖】 本题考查了二次函数的一般知识,求字母系数、解析式、顶点坐标;字母表示数(符号意识),数形结合思想,规律探究,合情推理,解题方法的灵活性等等,更重要的是一种胆识和魄力,敢不敢动手,会不会从简单,从特殊值入手去探究一般规律,画一画图帮助思考,所有这些都是做学问所必需的品质和素养,也是新课程改革所倡导的精神和最高境界.
【解题思路】 (1)将A0坐标代入y1的解析式可求得a1的值;a1的值知道了y1的解析式也就确定了,已知抛物线就可求出b1的值,又把(b1,0)代入y2,可求出a2 ,即得y2的解析式;(2)用同样的方法可求得a3 、a4 、a5 ……由此得到规律![]() ,所以顶点坐标满足的函数关系式是:y= x;(3)由(2)可知
,所以顶点坐标满足的函数关系式是:y= x;(3)由(2)可知![]() 得
得![]() ; 最后一问我们会猜测这是与直线y=x平行且过A(2,0)的一条直线,用特殊值法取
; 最后一问我们会猜测这是与直线y=x平行且过A(2,0)的一条直线,用特殊值法取 得
得 和
和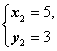 ,得所截得的线段长度为
,得所截得的线段长度为![]() ,换一组抛物线试试,求出的值也为
,换一组抛物线试试,求出的值也为![]() (当然用字母来运算就是解
(当然用字母来运算就是解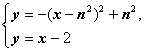 得
得 和
和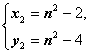 ,求得所截得的线段长度也为
,求得所截得的线段长度也为![]() ).
).
【解答过程】 略.
【方法规律】 掌握基础(知识),灵活运用(方法),敢于动手,不畏艰难.
【关键词】 二次函数 抛物线 规律探究


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
 已知抛物线y=-x2+mx-n的对称轴为x=-2,且与x轴只有一个交点.
已知抛物线y=-x2+mx-n的对称轴为x=-2,且与x轴只有一个交点.查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 已知抛物线y=ax2+bx+c过点C(0,3),顶点P(2,-1),直线x=m(m>3)交x轴于点D,抛物线交x轴于A、B两点(如图10).
已知抛物线y=ax2+bx+c过点C(0,3),顶点P(2,-1),直线x=m(m>3)交x轴于点D,抛物线交x轴于A、B两点(如图10).查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
查看答案和解析>>
科目:初中数学 来源: 题型:
| b |
| 2a |
| 4ac-b2 |
| 4a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com