
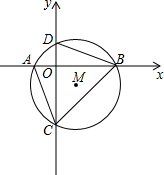
 如图,在直角坐标系中,半径为$\sqrt{5}$,圆心为M的⊙M经过A,B,C三点,已知点M的纵坐标为-1,点C的坐标为(0,3),OA:OB=1:3,⊙M与y轴交于点D
如图,在直角坐标系中,半径为$\sqrt{5}$,圆心为M的⊙M经过A,B,C三点,已知点M的纵坐标为-1,点C的坐标为(0,3),OA:OB=1:3,⊙M与y轴交于点D分析 (1)根据题意与图象可得点C的坐标,根据圆的性质可得点B的坐标,根据对称轴方程与点B的坐标;
(2)首先利用待定系数法确定二次函数的解析式,然后确定顶点E的坐标,从而求得CF=EF=1,从而说明△BCE是直角三角形;
(3)由抛物线的解析式可求得点A,E,B,C,D的坐标,判断Rt△BOD∽Rt△BCE,得∠CBE=∠OBD=β,因此sin(α-β)=sin(∠DBC-∠OBD)=sin∠OBC=$\frac{CO}{BC}$=$\frac{\sqrt{2}}{2}$;
(4)由于以P、A、C为顶点的三角形与△BCE相似,利用△BCE的特征得到△PAC为直角三角形,且两直角边的比为1:3,然后分类讨论:当∠APC=90°时,点P与点O重合,得到P点坐标为(0,0);当∠PAC=90°时,作AP1⊥AC交y轴于P1,如图,证明Rt△AOP1∽Rt△COA,利用相似比计算出OP1,得到P1的坐标;当∠ACP=90°时,作CP2⊥AC交y轴于P2,如图,证明Rt△COP2∽Rt△AOC利用相似比计算出OP2,得到P2的坐标.
解答 解:如图1,过点M作MN⊥x轴于点N,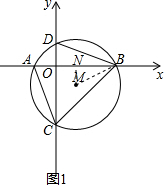
连接MB,则AN=BN,
在Rt△MNB中,$BN=\sqrt{B{M^2}-N{M^2}}$,
=$\sqrt{{{({\sqrt{5}})}^2}-1}=2$,
AB=4,
∵OA:OB=1:3,
∴$OA=\frac{1}{4}AB=\frac{1}{4}×4=1$,
∴A(-1,0),B(3,0),M(1,-1),
∵OB=OC=3,
AB⊥CD,∠AOC=∠DOB,
∠ACO=∠DBO,
∴△AOC≌△DOB,
∴DO=AO=1,
∴D(0,1);
(2)如图,设经过A,B,C三点的抛物线的解析式为y=a(x+1)(x-3),
将点(0,3)代入得,3=a(0+1)(0-3),
解得:a=1y=(x+1)(x-3)=x2-2x-3=(x-1)2-4,
抛物线的顶点坐标为(1,-4),
连接BE,CE,
过点E作EF⊥y轴,
可知OF=4,
∵OC=3,
CF=1,EF=1,
∴∠FCE=45°,
∴∠OCB=45°,
∴∠BCE=90°,
∴△BCE为直角三角形;
(3)如图2,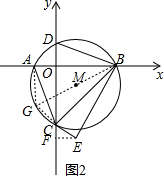
连接BM并延长交⊙M于点G,
连接AG,
BG为⊙M的直径,
则∠BCG=90°,∠GAB=90°,
∵∠BCE=90°,
∴G,C,E三点在同一条直线上,
可求得,BE=$2\sqrt{5}$
BG=$2\sqrt{5}$
∵BE=BG,BC=BC,
Rt△BGC≌Rt△BEC,
∠GBC=∠EBC,
∴∠ABG=45°-α,
Rt△ABG中,$AG=\sqrt{G{B^2}-A{B^2}}=\sqrt{{{({2\sqrt{5}})}^2}-{4^2}}$
=2,
∴sin(45°-β)=$\frac{2}{{2\sqrt{5}}}=\frac{{\sqrt{5}}}{5}$;
(4)存在.
∵以P、A、C为顶点的三角形与△BCE相似,
∴△PAC为直角三角形,且两直角边的比为1:3,
当∠APC=90°时,点P与点O重合,此时P点坐标为(0,0);
当∠PAC=90°时,作AP1⊥AC交y轴于P1,如图3,
∵∠P1AO+∠CAO=90°,
∠P1AO+∠AP1O=90°,
∴∠CAO=∠AP1O,
∴Rt△AOP1∽Rt△COA
∴OA2=OP1•OC,
∴OP1=$\frac{1}{3}$,
∴P1的坐标为(0,$\frac{1}{3}$);
当∠ACP=90°时,作CP2⊥AC交y轴于P2,如图3,
同样可证明Rt△COP2∽Rt△AOC得到OC2=OP2•OA,
∴OP2=9,
∴P2的坐标为(9,0),
综上所述,满足条件的P点坐标为(0,0),(0,$\frac{1}{3}$),(9,0).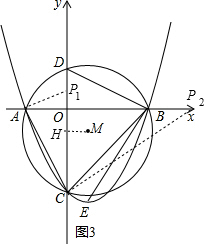
点评 本题考查了圆的综合题:熟练掌握圆的定义、垂径定理和相似三角形的判定与性质;会利用两点间的距离公式计算线段的长,综合性强,难度较大.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
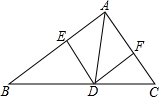 如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )
如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD平分∠BAC,那么四边形AEDF是矩形 | |
| D. | 如果AD⊥BC,且AB=AC,那么四边形AEDF是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com