
【题目】如图, ![]() 为⊙
为⊙![]() 的直径,
的直径, ![]() 、
、![]() 分别是⊙
分别是⊙![]() 的切线,切点为
的切线,切点为![]() 、
、![]() ,
, ![]() 、
、![]() 的延长线交于点
的延长线交于点![]() ,
, ![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.

(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,求⊙
,求⊙![]() 的半径.
的半径.
【答案】(1)证明见解析;
(2)⊙![]() 的半径
的半径![]() .
.
【解析】(1)连接OC,易证∠DPO=∠BPO,∠BPO=∠EDB,故∠DPO=∠EDB
(2)在直角三角形PBD中,由PB与DB的长,利用勾股定理求出PD的长,由切线长定理得到PC=PB,由PD-PC求出CD的长,在直角三角形OCD中,设OC=r,则有OD=8-r,利用勾股定理列出关于r的方程,求出方程的解得到r的值,
试题解析:(1)连接OC,易证∠DPO=∠BPO,∠BPO=∠EDB
∴∠DPO=∠EDB

(2)在Rt△PBD中,PB=3,DB=4,
根据勾股定理得:PD=![]() ,
,
∵PD与PB都为圆的切线,
∴PC=PB=3,
∴DC=PD-PC=5-3=2,
在Rt△CDO中,设OC=r,则有DO=4-r,
根据勾股定理得:(4-r)2=r2+22,
解得:r=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】定义:点A(x,y)为平面直角坐标系内的点,若满足x=y,则把点A叫做“平衡点”.例如:M(1,1),N(﹣2,﹣2)都是“平衡点”.当﹣1≤x≤3时,直线y=2x+m上有“平衡点”,则m的取值范围是( )
A.0≤m≤1
B.﹣3≤m≤1
C.﹣3≤m≤3
D.﹣1≤m≤0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,PE⊥PB,交CD与E,
(1)求证:PE=PD;
(2)当E为CD的中点时,求AP的长;
(3)设AP=x(![]() ),四边形BPEC的面积为y,求证:
),四边形BPEC的面积为y,求证: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
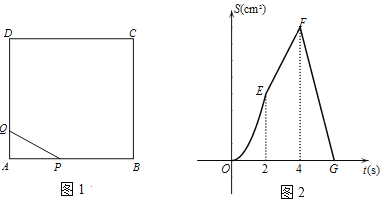
【题目】如图1,四边形![]() 是正方形,动点
是正方形,动点![]() 从点
从点![]() 出发,以
出发,以![]() cm/s的速度沿边
cm/s的速度沿边![]() 、
、![]() 、
、![]() 匀速运动到
匀速运动到![]() 终止;动点
终止;动点![]() 从
从![]() 出发,以
出发,以![]() cm/s的速度沿边
cm/s的速度沿边![]() 匀速运动到
匀速运动到![]() 终止,若
终止,若![]() 、
、![]() 两点同时出发,运动时间为
两点同时出发,运动时间为![]() s,△
s,△![]() 的面积为
的面积为![]() cm2.
cm2. ![]() 与
与![]() 之间函数关系的图像如图
之间函数关系的图像如图![]() 所示.
所示.
(1)求图![]() 中线段
中线段![]() 所表示的函数关系式;
所表示的函数关系式;
(2)当动点![]() 在边
在边![]() 运动的过程中,若以
运动的过程中,若以![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形,求
为顶点的三角形是等腰三角形,求![]() 的值;
的值;
(3)是否存在这样的![]() ,使
,使![]() 将正方形
将正方形![]() 的面积恰好分成
的面积恰好分成![]() 的两部分?若存在,求出这样的
的两部分?若存在,求出这样的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,顶点
,顶点![]() 的横坐标为
的横坐标为![]() .
.

(1)求二次函数的表达式及![]() 的坐标;
的坐标;
(2)若![]() (
(![]() )是
)是![]() 轴上一点,
轴上一点, ![]() ,将点
,将点![]() 绕着点
绕着点![]() 顺时针方向旋转
顺时针方向旋转![]() 得到点
得到点![]() .当点
.当点![]() 恰好在该二次函数的图像上时,求
恰好在该二次函数的图像上时,求![]() 的值;
的值;
(3)在(2)的条件下,连接![]() .若
.若![]() 是该二次函数图像上一点,且
是该二次函数图像上一点,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品进价为a元,商店将价格提高30%作零售价销售.在销售旺季过后,商店又以8折(即售价的80%)的价格开展促销活动.这时一件该商品的售价为( )
A.a元
B.0.8a元
C.1.04a元
D.0.92a元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD的边长为6,点E,F分别在边AD,边AB的延长线上,且DE=BF.
(1)如图1,连接CE,CF,EF,请判断△CEF的形状;
(2)如图2,连接EF交BD于M,当DE=2时,求AM的长;
(3)如图3,点G,H分别在边AB,边CD上,且GH=3![]() ,当EF与GH的夹角为45°时,求DE的长.
,当EF与GH的夹角为45°时,求DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com