
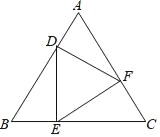
【题目】如图,D为等边△ABC的边AB上一点,且DE⊥BC,EF⊥AC,FD⊥AB,垂足分别为点E、F、D.若AB=6,则BE=_____.
【答案】2
【解析】
求出∠BDE=∠FEC=∠AFD=30°,求出∠DEF=∠DFE=∠EDF=60°,推出DF=DE=EF,即可得出等边三角形DEF,根据全等三角形性质推出三个三角形全等即可.求出AB=3BE,即可解答.
∵△ABC是等边三角形,
∴AB=AC=BC,∠B=∠C=∠A=60°,
∵DE⊥BC、EF⊥AC、FD⊥AB,
∴∠DEB=∠EFC=∠FDA=90°,
∴∠BDE=∠FEC=∠AFD=30°,
∴∠DEF=∠DFE=∠EDF=180°﹣90°﹣30°=60°,
∴DF=DE=EF,
∴△DEF是等边三角形,
在△ADF、△BED、△CFE中
∵∠ADF=∠BED=∠CFE,
∠A=∠B=∠C,
DF=DE=EF,
∴△ADF≌△BED≌△CFE,
∴AD=BE=CF,
∵∠DEB=90°,∠BDE=30°,
∴BD=2BE,
∴AB=3BE,
∴BE=![]() AB=2.
AB=2.
故答案为:2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,放在平面直角坐标系中的圆O的半径为3,现做如下实验:抛掷一枚均匀的正四面体骰子,它有四个顶点,各顶点数分别是1,2,3,4,每个顶点朝上的机会是相同的,连续抛掷两次,将骰子朝上的点数作为直角坐标系中点P的坐标(第一次的点数为横坐标,第二次的点数为纵坐标). 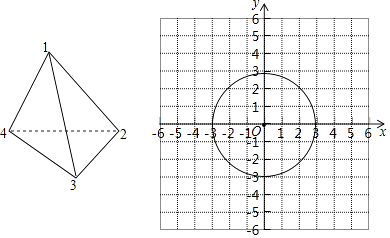
(1)若第一次骰子朝上的点数为1,第二次骰子朝上的点数为2,此时点P(填“是”或“否”)落在圆O内部;
(2)请你用树状图或列表的方法表示出P点坐标的所有可能结果;
(3)求点P落在圆O面上(含内部与边界)的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图所示,在△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于点E,与CD相交于点F.H是BC边上的中点,连接DH与BE相交于点G.
(1)求证:BF=AC;
(2)求证:CE=![]() BF;
BF;
(3)请你根据该题的条件并结合图形,自己提出一个问题,并解答或证明你提出的问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高高的路灯挂在路边的上方,高傲而明亮,小明拿着一根2米长的竹竿,想量一量路灯的高度,直接量是不可能的.于是,他走到路灯旁的一个地方,竖起竹竿(即AE),这时,他量了一下竹竿的影长(AC)正好是1米,他沿着影子的方向走,向远处走出两根竹竿的长度(即AB=4米),他又竖起竹竿,这时竹竿的影长正好是一根竹竿的长度(即BD=2米).此时,小明抬头瞧瞧路灯,若有所思地说:“噢,我知道路灯有多高了!”同学们,请你和小明一起解答这个问题:
(1)在图中作出路灯O的位置,并作OP⊥l于P.
(2)求出路灯O的高度,并说明理由.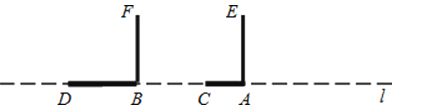
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB.
求证:CA+AD=BC.
小明为解决上面的问题作了如下思考:作△ADC关于直线CD的对称图形△A′DC,
∵CD平分∠ACB,∴A′点落在CB上,且CA′=CA,A′D=AD.因此,要证的问题转化为只要证A′D=A′B.请根据小明的思考写出该问题完整的证明过程.
(2)参照(1)中小明的思考方法,解答下列问题:
如图3,在四边形ABCD中,AC平分∠BAD,BC=CD=10,AC=17,AD=9,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家居专营店用2730元购进A、B两种新型玻璃保温杯共60个,这两种玻璃保温杯的进价、标价如表所示:
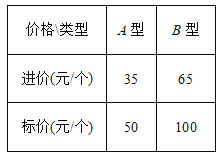
(1)这两种玻璃保温杯各购进多少个?
(2)若A型玻璃保温杯按标价的9折出售,B型玻璃保温杯按标价的8.5折出售,且在运输过程中有2个A型、1个B型玻璃保温杯不慎损坏,不能进行销售,请问这批玻璃保温杯全部售出后,该家居专营店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积 S(单位:m2)与工作时间 t(单位:h)之间的函数关系 如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
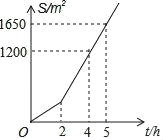
A. 150 m2 B. 300 m2 C. 330 m2 D. 450 m2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com