
分析 (1)摸到“10元“和“15元”时最多;
(2)画树状图和列表展示所有6种等可能的结果数,再找出所得购物券的金额不低于25元的结果数,然后根据概率公式求解.
解答 解:(1)该顾客最多可得到25元购物券;
故答案为25;
(2)画树状图为: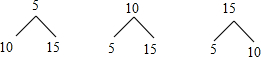
共有6种等可能的结果数,其中所得购物券的金额不低于25元的结果数为2,
所以该顾客所得购物券的金额不低于25元的概率=$\frac{2}{6}$=$\frac{1}{3}$.
或列表为: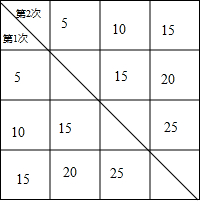
共有6种等可能的结果数,其中所得购物券的金额不低于25元的结果数为2,
所以该顾客所得购物券的金额不低于25元的概率=$\frac{2}{6}$=$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | a≥-1 | B. | a≤1 | C. | 0<a≤1 | D. | -1≤a≤0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
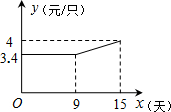 屈原食品公司接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只5元.为按时完成任务,该企业招收了新工人,设新工人小明第x天生产的粽子数量为n只,n与x满足如下关系式:$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}(0<x≤5)\\(5<x≤15)\end{array}$.
屈原食品公司接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只5元.为按时完成任务,该企业招收了新工人,设新工人小明第x天生产的粽子数量为n只,n与x满足如下关系式:$\left\{\begin{array}{l}n=45x\\ n=30x+90\end{array}\right.$$\begin{array}{l}(0<x≤5)\\(5<x≤15)\end{array}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数段(x分) | x≤10 | 11≤x≤15 | 16≤x≤20 | 21≤x≤25 | 26≤x≤30 |
| 人 数 | 10 | 15 | 35 | 112 | 128 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com