
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
【答案】(1)120 (2)C级人数为:120×30%=36人,D级人数为:120-36-24-48=12人 (3)36° (4)450份
【解析】试题分析:(1)根据A级人数为24人,以及在扇形图中所占比例为20%,24÷20%即可得出得出抽取的样本的容量;
(2)根据C级在扇形图中所占比例为30%,得出C级人数为:120×30%=36人,即可得出D级人数,补全条形图即可;
(3)根据A级和B级作品在样本中所占比例为:(24+48)÷120×100%=60%,即可根据用样本估计总体的方法得出该校这次活动共收到参赛作品750份,参赛作品达到B级以上的份数。
试题解析:
(1)∵A级人数为24人,在扇形图中所占比例为20%,
∴这次抽取的样本的容量为:24÷20%=120;
(2)根据C级在扇形图中所占比例为30%,得出C级人数为:120×30%=36人,
∴D级人数为:120-36-24-48=12人,
∴补充条形统计图如图所示:
(3)∵A级和B级作品在样本中所占比例为:(24+48)÷120×100%=60%,
∴该校这次活动共收到参赛作品750份,参赛作品达到B级以上有750×60%=450份。


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 过(﹣2,4),(﹣4,4)两点.
过(﹣2,4),(﹣4,4)两点.

(1)求二次函数![]() 的解析式;
的解析式;
(2)将![]() 沿x轴翻折,再向右平移2个单位,得到抛物线
沿x轴翻折,再向右平移2个单位,得到抛物线![]() ,直线y=m(m>0)交
,直线y=m(m>0)交![]() 于M、N两点,求线段MN的长度(用含m的代数式表示);
于M、N两点,求线段MN的长度(用含m的代数式表示);
(3)在(2)的条件下,![]() 、
、![]() 交于A、B两点,如果直线y=m与
交于A、B两点,如果直线y=m与![]() 、
、![]() 的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与
的图象形成的封闭曲线交于C、D两点(C在左侧),直线y=﹣m与![]() 、
、![]() 的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
的图象形成的封闭曲线交于E、F两点(E在左侧),求证:四边形CEFD是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有 (写出所有正确结论的序号)
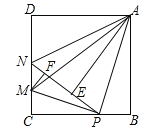
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为![]() ;
;
⑤当△ABP≌△ADN时,BP=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个周长为40厘米的正方形,从四个角各剪去一个正方形,做成一个无盖盒子.设这个盒子的底面积为y,剪去的正方形的边长为x,求有关y的二次函数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=BD;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
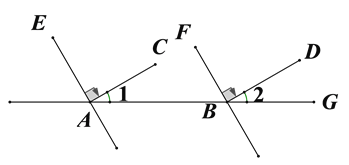
【题目】(8分)看图填空,并在括号内注明理由依据,
解: ∵∠1=30°, ∠2=30°
∴∠1=∠2
∴_______//________(_______________________________________)
又AC⊥AE(已知)
∴∠EAC=90°(______________)
∴∠EAB=∠EAC+∠1=120°
同理: ∠FBG=∠FBD+∠2=_________°.
∴∠EAB=∠FBG(_____________________________________).
∴______________//____________(同位角相等,两直线平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润 2000元。
该加工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨。受人员限制,两种加工方式不可同时进行。受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕。为此,该厂设计了两种可行方案:
方案一:尽可能多地制成奶片,其余直接销售鲜奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成。
你认为哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com