
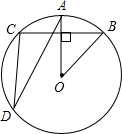
 如图,在⊙O中,弦BC=8cm,OA⊥BC,与⊙O交于点A,OA=4$\sqrt{2}$cm
如图,在⊙O中,弦BC=8cm,OA⊥BC,与⊙O交于点A,OA=4$\sqrt{2}$cm分析 (1)根据垂径定理可得$\widehat{AB}$=$\widehat{AC}$,再根据圆周角定理可得∠ADC=$\frac{1}{2}$∠AOB,进而可得答案;
(2)延长AO交⊙O于N,连接DN,AC,根据勾股定理列方程即可得到结论.
解答 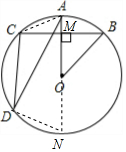 解:(1)∠OBC=2∠ADC,
解:(1)∠OBC=2∠ADC,
理由:设OA与BC于M,
∴OA⊥BC,
∴MB=$\frac{1}{2}$BC=4,
∴cos∠OBC=$\frac{\sqrt{2}}{2}$,
∴∠OBC=45°,
∴∠AOB=∠AOC=45°,
∴∠ADC=$\frac{1}{2}$∠AOC=22.5°,
∴∠OBC=2∠ADC;
(2)延长AO交⊙O于N,连接DN,AC,
∴AC2=CM2+AM2=42+(4$\sqrt{2}$-4)2=64-32$\sqrt{2}$,
∵CD∥OA,
∴DN=AC,
∴AD=$\sqrt{A{N}^{2}-D{N}^{2}}$=$\sqrt{128-64+32\sqrt{2}}$=64+32$\sqrt{2}$=4$\sqrt{4+2\sqrt{2}}$.
点评 此题主要考查了垂径定理,圆周角定理,以及勾股定理,关键是掌握垂直弦的直径平分这条弦,并且平分弦所对的两条弧.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
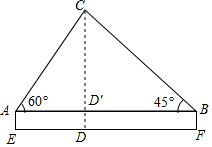 从相距100m的A,B两点观侧建筑物CD,用测角仪测得建筑物顶点CA体的高度的仰角分别为60°和45°,求E,F两点到建筑物底端D的距离分别为多少米.
从相距100m的A,B两点观侧建筑物CD,用测角仪测得建筑物顶点CA体的高度的仰角分别为60°和45°,求E,F两点到建筑物底端D的距离分别为多少米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sinB=$\frac{2}{3}$ | B. | cosB=$\frac{2}{3}$ | C. | tanB=$\frac{2}{3}$ | D. | 以上都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com