

分析 (1)由图可知,甲地到乙地距离900km,乙地与丙地距离150km,进而得到甲、丙间的距离;
(2)先求出列车到达丙地的时间,然后用待定系数法分别求出从甲到乙、从乙到丙时,y与x的函数关系式;
(3)分两种情况:①未到乙地时,离乙地的路程不超过100千米;②已过乙地,离乙地的路程不超过100千米;分别列出不等式求出x的范围即可.
解答 解:(1)由函数图象可知,当x=0时y=900,即刚出发时,甲与乙的距离为900千米,
当x=3时y=0,表示3小时后列车到达乙地,故列车速度为:900÷3=300千米/小时,
∵150÷300=0.5小时,∴0.5小时后列车到达丙地,乙与丙间的距离为150千米,
故甲、丙两地间的距离为:900+150=1050千米;
(2)当0≤x≤3时,设函数关系式为:y=k1x+b1,
将(0,900),(3,0)代入得:$\left\{\begin{array}{l}{{b}_{1}=900}\\{3{k}_{1}+{b}_{1}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-300}\\{{b}_{1}=900}\end{array}\right.$,
∴y=-300x+900;
当3≤x≤3.5时,设函数关系式为:y=k2x+b2,
将(3,0),(3.5,150)代入得:$\left\{\begin{array}{l}{3{k}_{2}+{b}_{2}=0}\\{3.5{k}_{2}+{b}_{2}=150}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=300}\\{{b}_{2}=-900}\end{array}\right.$,
∴y=300x-900;
综上,当0≤x≤3时,y=-300x+900;
当3≤x≤3.5时,y=300x-900;
(3)①当列车从甲到乙地的路程不超过100千米时,即当0≤x≤3时,
有:-300x+900≤100,解得:$\frac{8}{3}$≤x≤3;
②当列车从乙行驶到丙,到乙地的路程不超过100千米时,即当3≤x≤3.5时,
有:300x-900≤100,解得:3≤x≤$\frac{10}{3}$;
综上,当$\frac{8}{3}$≤x≤$\frac{10}{3}$时,高速列车离乙地的路程不超过100千米.
点评 本题主要考查一次函数的综合应用,结合题意读懂图象是前提,待定系数法求函数解析式是关键.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:解答题
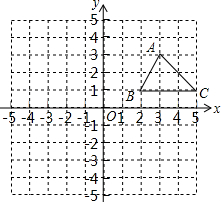 如图,△ABC的三个顶点在平面直角坐标系中的坐标分别为A(3,3),B(2,1),C(5,1),将△ABC绕点O逆时针旋转180°得△A′B′C′,请你在平面直角坐标系中画出△A′B′C′,并写出△A′B′C′的顶点坐标.
如图,△ABC的三个顶点在平面直角坐标系中的坐标分别为A(3,3),B(2,1),C(5,1),将△ABC绕点O逆时针旋转180°得△A′B′C′,请你在平面直角坐标系中画出△A′B′C′,并写出△A′B′C′的顶点坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 类比三角形中位线的定义,我们给出梯形中位线的定义:如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、DC的中点,称线段EF为梯形ABCD的中位线.
类比三角形中位线的定义,我们给出梯形中位线的定义:如图,在梯形ABCD中,AD∥BC,点E、F分别是AB、DC的中点,称线段EF为梯形ABCD的中位线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
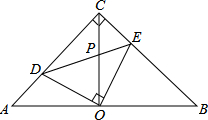 如图,在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,点D、E分别在AC、BC边上,且∠DOE=90°,DE交OC于P,下列结论:
如图,在等腰直角△ABC中,∠ACB=90°,O是AB边上的中点,点D、E分别在AC、BC边上,且∠DOE=90°,DE交OC于P,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,AC=8,E是AB中点,过点A作直线CD的垂线,垂足为D.
如图,△ABC中,∠ACB=90°,tanB=$\frac{4}{3}$,AC=8,E是AB中点,过点A作直线CD的垂线,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
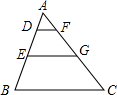 如图,已知D、E和F、G分别在△ABC的AB、AC上,DF∥EG∥BC,AD:DE:EB=1:2:3,则S梯形DEGF:S梯形EBCG=8:27.
如图,已知D、E和F、G分别在△ABC的AB、AC上,DF∥EG∥BC,AD:DE:EB=1:2:3,则S梯形DEGF:S梯形EBCG=8:27.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com