
| 2 |
| 3 |

| 3 |
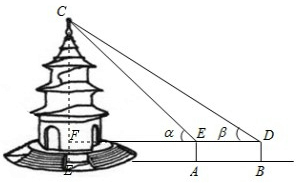 解:过点C作CE⊥AB于E,交DE于F,
解:过点C作CE⊥AB于E,交DE于F,| CF |
| tanα |
| x |
| tan45° |
| CF |
| tanβ |
| x |
| tan30° |
| 3 |
| 3 |
15(
| ||
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
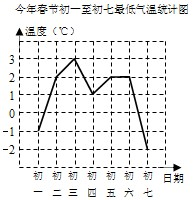 小华同学根据某地今年春节初一至初七的每天最低气温绘成了所示的折线统计图.关于这7天的每天最低气温的说法不正确的是( )
小华同学根据某地今年春节初一至初七的每天最低气温绘成了所示的折线统计图.关于这7天的每天最低气温的说法不正确的是( )| A、极差是5℃ |
| B、众数是2℃ |
| C、中位数是1℃ |
| D、平均数是1℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:
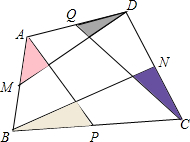 如图,在四边形ABCD中,M为AB的中点,P为BC的中点,N为CD的中点,Q为DA的中点,若图中中间的小四边形的面积为1,试求四个小三角形(阴影部分)面积之和.
如图,在四边形ABCD中,M为AB的中点,P为BC的中点,N为CD的中点,Q为DA的中点,若图中中间的小四边形的面积为1,试求四个小三角形(阴影部分)面积之和.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com