练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （）的相反数是（    ）．

    （A）            （B）             （C）            （D）


    A


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    下列运算正确的是（    ）

    (A)         (B)    (C)      (D)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感。他惊喜地发现：当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明。下面是小聪利用图1证明勾股定理的过程：

    将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：。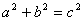

    证明：连结DB，过点D作BC边上的高DF，

    则DF=EC=，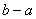

    ∵ ，

    又∵，

    ∴ ，

    ∴

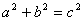
    请参照上述证法，利用图2完成下面的证明：

    将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°。

    求证：。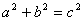

    证明：连结

    ∵

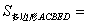
    又∵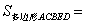

    ∴

    ∴ 。

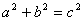    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，平行于BC的直线DE把△ABC分成的两部分面积相等.则=___________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


          

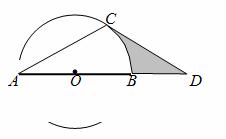
    如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°.

    (1)  求证：CD是⊙O的切线；[来源:]

    (2)  若⊙O的半径为2，求图中阴影部分的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算，结果是（    ）．

    （A）          （B）         （C）         （D）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    代数式有意义时，应满足的条件为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某商品先按批发价a元提高10%零售，后又按零售价降低10%出售，则最后的单价是

    A．a元                                                    B．0.99a元

    C．1.21a元                                              D．0.81a元

    查看答案和解析>>

    科目：初中数学 来源： 题型：


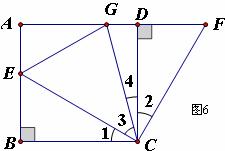
    如图6，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE。

    （1）求证：CE=CF；

    （2）若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？

         

    查看答案和解析>>

    同步练习册答案