
 OC。当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明。
OC。当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明。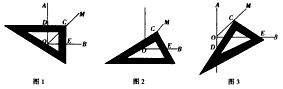
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
 ,1).
,1).查看答案和解析>>
科目:初中数学 来源: 题型:
 点P不与点O重合.
点P不与点O重合.
| ||
| 2 |
| GD |
| OD |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC.
如图,已知∠AOB=90°,∠AOC=60°,OD平分∠BOC,OE平分∠AOC.查看答案和解析>>
科目:初中数学 来源: 题型:
 (1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,求∠MON的度数;
(1)如图,已知∠AOB=90°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,求∠MON的度数;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com