
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①根据算术平方根的定义进行判断;
②根据平方根的定义进行判断;
③带根号的数不一定是无理数,开方开不尽的数是无理数;
④根据无理数的定义进行判断.
解答 解:①如果m是一个实数,m2的算术平方根是|m|,当m是非负数时,m2的算术平方根是m;
所以此说法不正确;
②如果m是一个正数,则-m没有平方根;所以此选项不正确;
③带根号的数不一定是无理数,如$\sqrt{4}$=2,是有理数;所以此选项说法不正确;
④无理数是无限不循环小数,所以无理数是无限小数,所以此选项说法正确;
所以本题说法正确的有1个:④,
故选B.
点评 此题主要考查了实数的定义、平方根及算术平方根的定义、无理数的定义.属于基础知识,熟练掌握这些基本概念是解题的关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
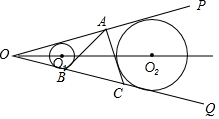 如图,已知⊙O1与⊙O2相离,OP和OQ是它们的两条外公切线,线段O1O2的垂直平分线交射线OP于A,过点A分别作⊙O1、⊙O2的切线,分别交射线OQ于B、C两点,求证:△ABC是等腰三角形.
如图,已知⊙O1与⊙O2相离,OP和OQ是它们的两条外公切线,线段O1O2的垂直平分线交射线OP于A,过点A分别作⊙O1、⊙O2的切线,分别交射线OQ于B、C两点,求证:△ABC是等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com