
科目:初中数学 来源: 题型:解答题
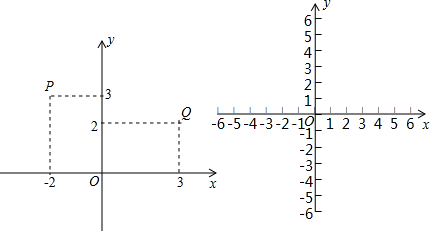
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 从一个装满黑球的布袋中摸出一个球是黑球 | |
| B. | 抛掷1枚普通硬币得到正面朝上 | |
| C. | 抛掷1颗正方体骰子得到的点数是偶数 | |
| D. | 抛掷1个普通图钉一定是针尖向下 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
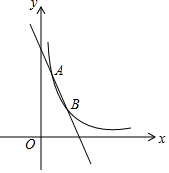 如图,一次函数y=kx+b与反比例函数y=$\frac{12}{x}$(x>0)的图象交于A(m,6),B(n,3)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{12}{x}$(x>0)的图象交于A(m,6),B(n,3)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
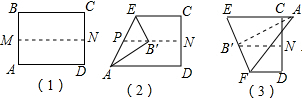
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC是直角三角形,∠ACB=90°.
如图,△ABC是直角三角形,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
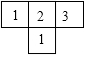 由7个大小相同的小正方体组合成一个几何体.其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )
由7个大小相同的小正方体组合成一个几何体.其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )| A. |  | B. |  | C. |  | D. | 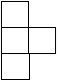 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
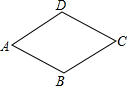 如图,广场中心的菱形花坛ABCD的周长是40米,∠A=60°,则A,C两点之间的距离为( )
如图,广场中心的菱形花坛ABCD的周长是40米,∠A=60°,则A,C两点之间的距离为( )| A. | 5米 | B. | 5$\sqrt{3}$米 | C. | 10米 | D. | 10$\sqrt{3}$米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com