
����Ŀ��ij��ѧ��չ��������д���������Ϊ�˽�ѧ���IJ���������ڸ�У�����ȡ���ĸ��༶ѧ�����е��飬���ռ����������������Ƴ�ͼ1��ͼ2�����в�������ͳ��ͼ�������ͼ�е���Ϣ������������⣺
��1�����ĸ�����������ѧ����__________�ˣ�
��2�����㲹ȫ����ͳ��ͼ��
��3����ͼ1�мװ�����Ӧ������Բ�ĽǵĶ�����
��4�����ĸ��༶��ѧ��������160�ˣ�ȫУ��2000�ˣ��������ȫУ��ѧ���в�����λ�Ĵ�Լ�ж�����.

���𰸡���1��100����2������������3��108������4��1250.
��������
�����������1�������Ұ����30�ˣ���ռ��Ϊ20%������������ĸ�����������
��2�����ݶ������35�ˣ���������100���������������ռ�İٷֱȣ���������1��ȥ������ռ�İٷֱȣ����ɵó�����ռ�İٷֱȣ��ٳ��Բ����������������ɵó�����������������Ӷ���ȫͳ��ͼ��
��3�����ݼװ༶��ռ�İٷֱȣ��ٳ���360�㣬���ɵó��𰸣�
��4�����������������壬�ɵô𰸣�
�����������1�����ĸ�����������ѧ�����ǣ�
30��30%=100���ˣ���
�ʴ�Ϊ100��
��2������ռ�İٷֱ��ǣ�![]() ��100%=35%��
��100%=35%��
����ռ�İٷֱ��ǣ�1��30%��20%��35%=15%��
�����������ǣ�100��15%=15���ˣ���
��ͼ��

��3���װ༶����Ӧ������Բ�ĽǵĶ����ǣ�30%��360��=108�㣻
��4����������ã�2000��![]() =1250���ˣ���
=1250���ˣ���
��ȫУ��ѧ���в�����λ�Ĵ�Լ��1250�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˷ḻУ�Ļ����ٽ�ѧ��ȫ�淢չ.����ij����������ȫ����Сѧ��չ���鷨����������÷Ϸ��У���������3�·ݣ�����ijУ�����ˡ���÷Ϸ���ݳ������������ɼ�����ΪA��B��C��D��E����ȼ�����У����ѧ���μ���ѧУ�ı�������������������Ƴ�����������������ͳ��ͼ�������ͼ����Ϣ�������������.

��1�����У�μӱ��Ρ���÷Ϸ���ݳ�������ѧ��������
��2��������ͳ��ͼB�ȼ�����Ӧ���ε�Բ�ĽǶ�����
��3����֪A�ȼ���4��ѧ������1��������3��Ů�����ִ�������ѡȡ2��ѧ����ΪȫУѵ����ʾ���ߣ��������б�������״ͼ�ķ��������ǡ��ѡ1��������1��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ɶ������ض��������֤����������������в�ͬ�����е��������������С������У�����ϲ�ķ��֣�������ȫ�ȵ�ֱ����������ͼ1��ͼ2�ڷ�ʱ���������������������֤����������С������ͼ1֤�����ɶ����Ĺ��̣�
������ȫ�ȵ�ֱ�������ΰ�ͼ1��ʾ�ڷţ�������DAB=90������֤��a2+b2=c2.
֤��������DB������D��BC���ϵĸ�DF����DF=EC=b��a��
��S�ı���ADCB=S��ACD+S��ABC= 12 b2+ 12 ab��
����S�ı���ADCB=S��ADB+S��DCB= 12 c2+ 12 a��b��a��
�� 12 b2+ 12 ab= 12 c2+ 12 a��b��a��
��a2+b2=c2
���������֤��������ͼ2��������֤����
������ȫ�ȵ�ֱ�������ΰ�ͼ2��ʾ�ڷţ�������DAB=90������֤��a2+b2=c2 ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �ֱ�����
�ֱ�����![]() ��
��![]() Ϊб�ߵ�ֱ�������Σ�
Ϊб�ߵ�ֱ�������Σ�![]() ��
��![]() �ǵȱ�������.
�ǵȱ�������.
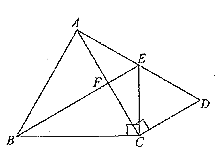
��1����֤��![]() ��
��
��2����![]() ����
����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ���ס���������![]() �س���������ͬ·��ǰ��ͬһĿ�ĵأ�;�о���
�س���������ͬ·��ǰ��ͬһĿ�ĵأ�;�о���![]() ��.�׳��ȳ��������׳�����
��.�׳��ȳ��������׳�����![]() ��ʱ���ҳ���ʼ����.���ҳ�����
��ʱ���ҳ���ʼ����.���ҳ�����![]() ��ʱ���׳���
��ʱ���׳���![]() �����
�����![]() .��ס���������
.��ס���������![]() ��֮��ľ���Ϊ��
��֮��ľ���Ϊ��![]() ��
��![]() ���ҳ���ʻ��ʱ��Ϊ
���ҳ���ʻ��ʱ��Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �ĺ�����ϵ��ͼ����ʾ.
�ĺ�����ϵ��ͼ����ʾ.
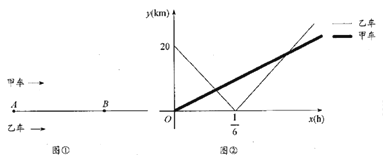
��1��![]() ��
��![]() ����֮��ľ���Ϊ
����֮��ľ���Ϊ ![]() ��
��
��2����![]() Ϊ��ֵʱ���ס����������
Ϊ��ֵʱ���ס����������![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪����������![]() ��һ�κ���
��һ�κ���![]() ��ͼ���ڵ�A.
��ͼ���ڵ�A.
��1�����A�����ꣻ
��2����x����һ��P��a��b��������P��x��Ĵ��ߣ�����λ�ڵ�A���Ҳࣩ���ֱ�![]() ��
��![]() ��ͼ���ڵ�B��C������OC����BC=
��ͼ���ڵ�B��C������OC����BC=![]() OA������OBC�����.
OA������OBC�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
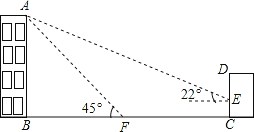
����Ŀ����ͼ����ԥ��ijУ��ѧ¥AB�ĺ�����һ������CD�������������ļн���22��ʱ����ѧ¥�ڽ������ǽ�����¸�3��Ӱ��CE���������������н���45��ʱ����ѧ¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��30�ľ��루B��F��C��һ��ֱ���ϣ�.
��1�����ѧ¥AB�ĸ߶ȣ�
��2����Ҫ��A��E֮���һЩ���죬�������A��E֮��ľ���.�������ȷ��lm�����ο����ݣ�sin22����![]() ��cos22���
��cos22���![]() ��tan22���
��tan22���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����6���ʵغʹ�С����ͬ����ÿ����ֻ����һ�����֣�������3,4,5���������������У�����4,5,6����������������У�
(1)С��Ӽ��������ģ��һ����������������������3�������ĸ��ʣ�
(2)С��Ӽ����С�С���������и����������һ������С���������ϵ����ֱ�С���������ϵ����ִ�1�����С������ʤһ�������������б���(����״ͼ)��С������ʤһ�����ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
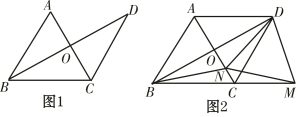
����Ŀ����֪����ABC�ǵȱ������Σ�����C��CD��AB����CD��AB������BD��AC�ڵ�O��
��1����ͼ1����֤��AC��ֱƽ��BD��
��2����ͼ2����M��BC���ӳ����ϣ���N���߶�CO�ϣ���ND��NM������BN����֤��NB��NM��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com