
【题目】如图,已知点A、B、C在同一直线上,△ABD和△BCE都是等边三角形.则在下列结论中:①AP=DQ,②EP=EC,③PQ=PB,④∠AOB=∠BOC=∠COE.正确的结论是(填写序号). 
【答案】①③④
【解析】解:∵△ABD和△BCE都是等边三角形, ∴BD=BA=AD,BE=BC=EC,∠ABD=∠CBE=60°,
∵点A、B、C在同一直线上,
∴∠DBE=180°﹣60°﹣60°=60°,
∴∠ABE=∠DBC=120°.
在△ABE和△DBC中, ,
,
∴△ABE≌△DBC,
∴∠BAE=∠BDC.
在△ABP和△DBQ中, ,
,
∴△ABP≌△DBQ,
∴AP=DQ,BP=BQ.
∴①正确.
∵∠PBQ=60°,
∴△BPQ是等边三角形,
∴PQ=PB.∠BPQ=60°.
∴③正确.
∵∠EPB>∠BPQ,∠BPQ=∠EBP=60°,
∴∠EPB>∠EBP,
∴EB>EP,
∴EC>EP,
∴②不正确.
∵∠DPA=∠PDO+∠DOP,∠DPA=∠PAB+∠ABP,∠PDO=∠PAB,
∴∠DOP=∠ABP=60°,
∴∠COE=60°,∠AOC=120°.
∵△ABE≌△DBC,
∴S△ABE=S△DBC , AE=DC,
∴点B到AE、DC的距离相等,
∴点B在∠AOC的角平分线上,
∴∠AOB=∠BOC= ![]() ∠AOC=60°,
∠AOC=60°,
∴∠AOB=∠BOC=∠COE=60°.
∴④正确.
故答案为①③④.
易证△ABE≌△DBC,则有∠BAE=∠BDC,从而可证到△ABP≌△DBQ,则有AP=DQ,BP=BQ,由∠PBQ=60°可得△BPQ是等边三角形,则有PQ=PB.∠BPQ=60°,从而可得∠EPB>∠EBP,即可得到EB>EP,即EC>EP,由△ABE≌△DBC可得S△ABE=S△DBC , AE=DC,从而可得点B到AE、DC的距离相等,因而点B在∠AOC的角平分线上,即可得到∠AOB=∠BOC=∠COE=60°.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=120°,AB=AC=6.P是底边BC上的一个动点(P与B、C不重合),以P为圆心,PB为半径的⊙P与射线BA交于点D,射线PD交射线CA于点E.
(1)若点E在线段CA的延长线上,设BP=x,AE=y,求y关于x的函数关系式,并写出x的取值范围.
(2)当BP=![]() 时,试说明射线CA与⊙P是否相切.
时,试说明射线CA与⊙P是否相切.
(3)连接PA,若S△APE=![]() S△ABC,求BP的长.
S△ABC,求BP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,C是线段BE上一点,以BC、CE为边分别在BE的同侧作等边△ABC和等边△DCE,连结AE、BD. 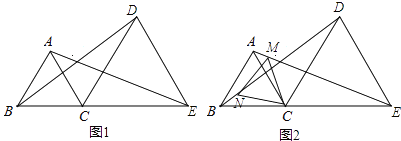
(1)求证:BD=AE;
(2)如图2,若M、N分别是线段AE、BD上的点,且AM=BN,请判断△CMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( ).
A.两条对角线垂直且相等的四边形是正方形
B.两条对角线互相垂直的四边形是菱形
C.两条对角线互相平分且相等的四边形是矩形
D.一组对边平行,另一组对边相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形OABC中,O为直角坐标系的原点,A、B、C的坐标分别为(14,0)、(14,3)、(4,3).点P、Q同时从原点出发,分别作匀速运动,其中点P沿OA向终点A运动,速度为每秒1个单位;点Q沿OC、CB向终点B运动,当这两点中有一点到达自己的终点时,另一点也停止运动.设P从出发起运动了t秒.
(1)如果点Q的速度为每秒2个单位,①试分别写出这时点Q在OC上或在CB上时的坐标(用含t的代数式表示,不要求写出t的取值范围);
②求t为何值时,PQ∥OC?
(2)如果点P与点Q所经过的路程之和恰好为梯形OABC的周长的一半,①试用含t的代数式表示这时点Q所经过的路程和它的速度;
②试问:这时直线PQ是否可能同时把梯形OABC的面积也分成相等的两部分?如有可能,求出相应的t的值和P、Q的坐标;如不可能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com