
【题目】(1)将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.观察图2可知:与BC相等的线段是 ,∠CAC′= °.

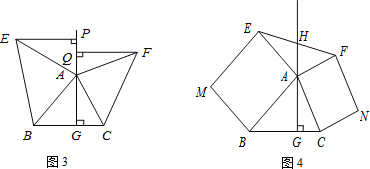
(2)如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.
(3)如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H.若AB=kAE,AC=kAF,试探究HE与HF之间的数量关系,说明理由.
【答案】(1)A′D;=90°;(2)EP=FQ;见解析(3)HE=HF
【解析】解:(1)如图2,由旋转的性质可知,△ABC≌△A′C′D,
∴BC=A′D,∠ACB=∠C′AD,又∠ACB+∠CAB=90°,
∴∠C′AD+∠CAB=90°,即∠CAC′=90°,
故答案为:A′D;=90°;
(2)EP=FQ,
证明:∵△ABE是等腰直角三角形,
∴∠EAB=90°,即∠EAP+∠BAG=90°,又∠ABG+∠BAG=90°,
∴∠EAP=∠ABG,
在△APE和△BGA中,
 ,
,
∴△APE≌△BGA,
∴EP=AG,
同理,FQ=AG,
∴EP=FQ;
(3)HE=HF,
证明:作EP⊥GA交GA的延长线于P,作FQ⊥GA交GA的延长线于Q,
∵四边形ABME是矩形,
∴∠EAB=90°,即∠EAP+∠BAG=90°,又∠ABG+∠BAG=90°,
∴∠EAP=∠ABG,又∠APE=∠BGA=90°,
∴△APE∽△BGA,
∴![]() =
=![]() ,即AG=kEP,
,即AG=kEP,
同理△AQF∽△CGA,
∴![]() =k,即AG=kFQ,
=k,即AG=kFQ,
∴EP=FQ,
∵EP⊥GA,FQ⊥GA,
∴EP∥FQ,又EP=FQ,
∴HE=HF.



科目:初中数学 来源: 题型:
【题目】我国最长的河流长江全长约为6300千米,用科学记数法表示为( )
A. 63×102米 B. 6.3×103米 C. 6.3×106米 D. 6.3×105米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
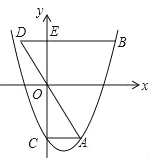
(1)用含m的代数式表示BE的长.
(2)当m=![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=-5x2+8x-1,下列说法中正确的是( )
A. 有最小值2.2 B. 有最大值2.2 C. 有最小值-2.2 D. 有最大值-2.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种感冒病毒的直径为0.0000000031米,用科学记数法表示为 ( )
A. 3.1×10-8米B. 3.1×10-9米C. 3.1×109米D. 3.1×108米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com