
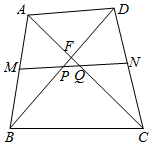
 如图,四边形ABCD的对角线AC,BD相交于点F,M,N分别为AB,CD的中点,连接MN分别交BD,AC于点P,Q,且∠FPQ=∠FQP,若BD=9,则AC=9.
如图,四边形ABCD的对角线AC,BD相交于点F,M,N分别为AB,CD的中点,连接MN分别交BD,AC于点P,Q,且∠FPQ=∠FQP,若BD=9,则AC=9. 分析 取线段BC的中点E,连接EM、EN,由三角形中位线定理即可得出ME∥AC、ME=$\frac{1}{2}$AC、NE∥BD、NE=$\frac{1}{2}$BD=$\frac{9}{2}$,再根据平行线的性质即可得出∠EMN=∠FQP、∠ENM=∠FPQ,结合∠FPQ=∠FQP即可得出∠EMN=∠ENM,从而得出ME=NE=$\frac{9}{2}$,由ME=$\frac{1}{2}$AC即可求出AC的长度.
解答 解:取线段BC的中点E,连接EM、EN,如图所示.
∵M、N,E分别为AB,CD,BC的中点,
∴ME∥AC,ME=$\frac{1}{2}$AC,NE∥BD,NE=$\frac{1}{2}$BD=$\frac{9}{2}$,
∴∠EMN=∠FQP,∠ENM=∠FPQ.
又∵∠FPQ=∠FQP,
∴∠EMN=∠ENM.
∴ME=NE=$\frac{9}{2}$.
∴AC=2ME=9.
故答案为:9.
点评 本题考查了三角形中位线定理、平行线的性质以及等腰三角形的性质,根据三角形中位线定理结合平行线的性质找出∠EMN=∠ENM是解题的关键.


科目:初中数学 来源: 题型:解答题
 随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:
随着车辆的增加,交通违规的现象越来越严重,交警对人民路某雷达测速区检测到的一组汽车的时速数据进行整理(速度在30-40含起点值30,不含终点值40),得到其频数及频率如表:| 数据段 | 频数 | 频率 |
| 30-40 | 10 | 0.05 |
| 40-50 | 36 | c |
| 50-60 | a | 0.39 |
| 60-70 | b | d |
| 70-80 | 20 | 0.10 |
| 总计 | 200 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
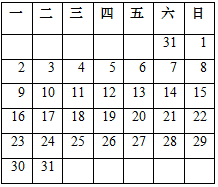 如图是2017年1月份的日历,在日历上任意圈出一个竖列上相邻的3个数.如果被圈出的三个数的和为63,则这三个数中最后一天为2017年1月28号.
如图是2017年1月份的日历,在日历上任意圈出一个竖列上相邻的3个数.如果被圈出的三个数的和为63,则这三个数中最后一天为2017年1月28号.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com