
 如图,将△ABC绕顶点C旋转得到△A′B′C,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠ABC等于( )
如图,将△ABC绕顶点C旋转得到△A′B′C,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠ABC等于( )| A. | 40° | B. | 55° | C. | 65° | D. | 70° |
分析 由旋转的性质得△ABC≌△A′B′C得∠A′=∠A=25°、CB=CB′、∠ABC=∠B′,根据∠BCA′=45°得∠CBB′=∠BCA′+∠A′=45°+25°=70°,继而由∠ABC=∠B′=∠CBB′=70°可得答案.
解答 解:∵△ABC绕顶点C旋转得到△A′B′C,
∴△ABC≌△A′B′C,
∴∠A′=∠A=25°,CB=CB′,∠ABC=∠B′,
∵∠BCA′=45°,
∴∠CBB′=∠BCA′+∠A′=45°+25°=70°,
∴∠ABC=∠B′=∠CBB′=70°,
故选:D.
点评 本题主要考查旋转的性质、三角形的外角性质及等边对等角的应用,熟练掌握旋转的性质得出对应角相等、对应边相等是解题的关键.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
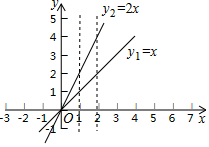 小华在研究函数y1=x与y2=2x图象关系时发现:如图所示,当x=1时,y1=1,y2=2;当x=2时,y1=2,y2=4;…;当x=a时,y1=a,y2=2a.他得出如果将函数y1=x图象上各点的横坐标不变,纵坐标变为原来的2倍,就可以得到函数y2=2x的图象.类比小华的研究方法,解决下列问题:
小华在研究函数y1=x与y2=2x图象关系时发现:如图所示,当x=1时,y1=1,y2=2;当x=2时,y1=2,y2=4;…;当x=a时,y1=a,y2=2a.他得出如果将函数y1=x图象上各点的横坐标不变,纵坐标变为原来的2倍,就可以得到函数y2=2x的图象.类比小华的研究方法,解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
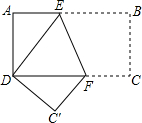 在长方形纸片ABCD中,AD=6cm,AB=8cm,按如图方式折叠,使点B与点D重合,折痕为EF,则EF的长为$\frac{15}{2}$.
在长方形纸片ABCD中,AD=6cm,AB=8cm,按如图方式折叠,使点B与点D重合,折痕为EF,则EF的长为$\frac{15}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com