

���� ��1����ȫ�������ε����ʿ�֪AM=MD=4���ɴ˵õ�2t=4�������t��ֵ��
��2������A��AG��BC������ΪG����Rt��ABG����������������Ǻ���ֵ�����AG�ij���������ɵõ�AM=8-2t��Ȼ���١�AEM����������������Ǻ���ֵ�����AE��ME�ij����������y=S��ANM�ɵõ�y��x�ĺ�����ϵʽ��
��3�����˶�ʱ��Ϊt��ʱ����ANM�������?ABCD�����$\frac{3}{8}$�����������з�����⼴�ɣ�
��4����A��AG��BC������ΪG������t=$\frac{8}{3}$������AO��NC�ij������֤����AOP�ס�CNP�������QO=x���������������ε����ʿ����OP�ij���
��� �⣺��1�����ı���ABCDΪƽ���ı��Σ�
��AD=BC=8��
�ߡ�AEM�ա�DFM��
��AM=MD=4��
��2t=4��
��t=2��
��2����ͼ1������A��AG��BC������ΪG��
�ߡ�AGB=90�㣬��A=60�㣬
��AG=$\frac{\sqrt{3}}{2}$AB=2$\sqrt{3}$��
��MD=2t��
��AM=8-2t��
��y=S��ANM=$\frac{1}{2}$����8-2t����2$\sqrt{3}$=-2$\sqrt{3}$t+8$\sqrt{3}$��
��3�����˶�ʱ��Ϊt��ʱ����ANM�������?ABCD�����$\frac{3}{8}$��
���������-2$\sqrt{3}$t+8$\sqrt{3}$=$\frac{3}{8}$��8��2$\sqrt{3}$��
������2$\sqrt{3}$=2$\sqrt{3}$t��
���t=1��
�ʵ�t=1ʱ����ANM�������?ABCD�����$\frac{3}{8}$��
��4����ͼ����A��AG��BC������ΪG��
��AB��CD��MF��CD��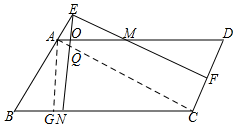
��MF��AB��
���MEA=90�㣬
��AD��BC��
���EAM=��B=60�㣬
�ɣ�2���ɵã�AM=8-2t��
��AE=$\frac{1}{2}$AM=4-t��
��BE=AB+AE=8-t��
�ߡ�B=60�㣬EN��BC��AG��BC��
��BN=$\frac{1}{2}$BE=4-$\frac{1}{2}$t��BG=$\frac{1}{2}$AB=2��
��t=$\frac{8}{3}$ʱ��GN=BN-BG=$\frac{2}{3}$��EN��BC��
��AO=$\frac{2}{3}$��NC=8-2-$\frac{2}{3}$=$\frac{16}{3}$��
��QO=x����QN=2$\sqrt{3}$-x��
��AO��NC��
���AOQ�ס�CNQ��
��$\frac{OA}{NC}$=$\frac{OQ}{NQ}$����$\frac{\frac{2}{3}}{\frac{16}{3}}$=$\frac{x}{2\sqrt{3}-x}$��
��ã�x=$\frac{2\sqrt{3}}{9}$��
��OQ�ij�Ϊ$\frac{2\sqrt{3}}{9}$��
���� ������Ҫ��������ı��ε��ۺ�Ӧ�ã������ʱ��Ҫ����ȫ�������ε��ж������ʡ���30��ǵ�ֱ�������ε����ʡ������ε������ʽ�����������ε����ʺ��ж��ȣ��ú�t��ʽ�ӱ�ʾ����߶εij��ȣ��������������εĶ�Ӧ�߳ɱ����г�����ʽ�ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
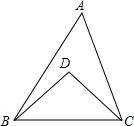 ��ͼ��ʾ���ڡ�ABC�У���A=60�㣬��D�ڡ�ABC���ڲ������ҡ�DBA=$\frac{1}{4}$��ABC����DCA=$\frac{1}{4}$��ACB�����D�Ķ�����90�㣮
��ͼ��ʾ���ڡ�ABC�У���A=60�㣬��D�ڡ�ABC���ڲ������ҡ�DBA=$\frac{1}{4}$��ABC����DCA=$\frac{1}{4}$��ACB�����D�Ķ�����90�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ھ���ABCD�У�AB=6cm��BC=12cm����P�ӵ�A������AB��1cm/s���ٶ����յ�B�ƶ���ͬʱ����Q�ӵ�B������BC��2cm/s���ٶ����C�ƶ���������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������P�˶���ʱ��Ϊts��
��ͼ���ھ���ABCD�У�AB=6cm��BC=12cm����P�ӵ�A������AB��1cm/s���ٶ����յ�B�ƶ���ͬʱ����Q�ӵ�B������BC��2cm/s���ٶ����C�ƶ���������һ�㵽���յ�ʱ����һ��Ҳֹͣ�˶������P�˶���ʱ��Ϊts���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com