
【题目】在△ABC中,∠C=90°,BD是△ABC的角平分线,P是射线AC上任意一点(不与A、D、C三点重合),过点P作PQ⊥AB,垂足为Q,交直线BD于E. 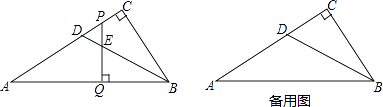
(1)如图,当点P在线段AC上时,说明∠PDE=∠PED.
(2)作∠CPQ的角平分线交直线AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由.
【答案】
(1)解:∵PQ⊥AB,
∴∠EQB=∠C=90°,
∴∠BEQ+∠EBQ=90°,∠CBD+∠PDE=90°,
∵BD为∠ABC的平分线,
∴∠CBD=∠EBQ,
∵∠PED=∠BEQ,
∴∠PDE=∠PED
(2)解:当P在线段AC上时,如图1所示,此时PF∥BD,
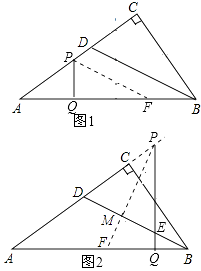
理由为:∵∠PDE=∠PED,
∴PD=PE,
∵PF为∠CPQ的平分线,∠CPQ为△PDE的外角,
∴∠CPF=∠QPF=∠PDE=∠PED,
∴PF∥BD;
当P在线段AC延长线上时,如图2所示,PF⊥BD,
理由为:∵∠PDE=∠PED,
∴PD=PE,
∵PM为∠CPQ的平分线,
∴PF⊥BD
【解析】(1)由PQ与AB垂直,得到一对直角相等,理由直角三角形的两锐角互余得到两对角互余,再BD为角平分线,利用角平分线定义得到一对角相等,再由对顶角相等,利用等量代换即可得证;(2)分两种情况,当P在线段AC上时,如图1所示,可得出PF与BD平行,由第一问的结论利用等角对等边得到PD=PE,利用角平分线定义及外角性质得到一对内错角相等,利用内错角相等两直线平行即可得证;当P在AC延长线时,PF垂直于BD,由PD=PE,利用三线合一即可得证.
【考点精析】本题主要考查了平行线的判定和三角形的内角和外角的相关知识点,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】两条平行直线上各有n个点,用这n对点按如下的规则连接线段;
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出;
图1展示了当n=1时的情况,此时图中三角形的个数为0;
图2展示了当n=2时的一种情况,此时图中三角形的个数为2;
(1)当n=3时,请在图3中画出使三角形个数最少的图形,此时图中三角形的个数为__________个;
(2)试猜想当n对点时,按上述规则画出的图形中,最少有多少个三角形?
(3)当n=2006时,按上述规则画出的图形中,最少有多少个三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE=°;
(2)如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
(3)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )

A.6 B.8 C.9 D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】台风是一种自然灾害,它以台风中心为圆心在周围上千米的范围内形成极端气候,有极强的破坏力。如图,有一台风中心沿东西方向AB由点A行驶向点B,已知点 C为一海港,且点 C与直线 AB上两点A,B的距离分别为300km和400km,又 AB=500km,以台风中心为圆心周围250km以内为受影响区域。

(1)海港C受台风影响吗?为什么?
(2)若台风的速度为20km/h,台风影响该海港持续的时间有多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com